
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①BE=DF;②∠AEB=75°;③CE=2;④S正方形ABCD=2+![]() ,其中正确答案是( )
,其中正确答案是( )

A.①②B.②③C.①②④D.①②③
【答案】C
【解析】
证明Rt△ABE≌Rt△ADF,根据全等三角形的性质得到BE=DF;根据等腰直角三角形的性质、等边三角形的性质求出∠AEB;根据等腰直角三角形的性质求出CE;根据勾股定理求出正方形的边长.
∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,①说法正确;
∵CB=CD,BE=DF,
∴CE=CF,即△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,②说法正确;
如图,∵△CEF为等腰直角三角形,EF=2,
∴CE=![]() ,③说法错误;
,③说法错误;
设正方形的边长为a,则DF=a-![]() ,
,
在Rt△ADF中,
AD2+DF2=AF2,即a2+(a-![]() )2=4,
)2=4,
解得a=![]() 或a=
或a=![]() (舍去),
(舍去),
则a2=2+![]() ,即S正方形ABCD=2+
,即S正方形ABCD=2+![]() ,④说法正确,
,④说法正确,
故选C.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=10,BC=12,矩形DEFG中,EF=4,FG>12.
(1)如图①,点A是FG的中点,FG∥BC,将矩形DEFG向下平移,直到DE与BC重合为止.要研究矩形DEFG与△ABC重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).
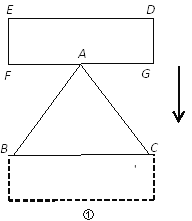
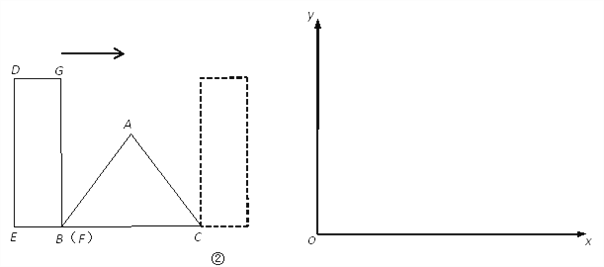
(2)如图②,点B与F重合,E、B、C在同一直线上,将矩形DEFG向右平移,直到点E与C重合为止.设矩形DEFG与△ABC重叠部分的面积为y,平移的距离为x.
① 求y与x的函数关系式,并写出自变量的取值范围;
② 在给定的平面直角坐标系中画出y与x的大致图象,并在图象上标注出关键点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形 OABC 的 顶 点 A(0,3),C(- 1,0). 将 矩 形 OABC 绕原点顺时针旋转 900,得到矩形 OA’B’C’.解答下列问题:
(1)求出直线 BB’的函数解析式;
(2)直线 BB’与 x 轴交于点 M、与 y 轴交于点N,抛物线 y = ax2+ bx + c 的图象经过点C、M、N,求抛物线的函数解析式.
(3)将△MON 沿直线 MN 翻折,点 O 落在点P 处,请你判断点 P 是否在抛物线上,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A、O两点的坐标分别为(2,0),(0,0),点P在正比例函数y=x(x>0)图象上运动,则满足△PAO为等腰三角形的P点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
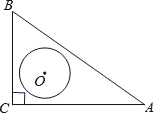
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
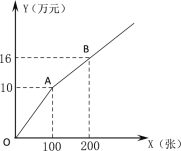
【题目】某演唱会购买门票的方式有两种.
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;
方式二:如图所示.
设购买门票x张,总费用为y万元,方式一中:总费用=广告赞助费+门票费.
(1)求方式一中y与x的函数关系式.
(2)若甲、乙两个单位分别采用方式一、方式二购买本场演唱会门票共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人约好步行沿同一路线同一方向在某景点集合,已知甲乙二人相距660米,二人同时出发,走了24分钟时,由于乙距离景点近,先到达等候甲,甲共走了30分钟也到达了景点与乙相遇.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的关系如图所示,下列说法错误的是( )
(分钟)之间的关系如图所示,下列说法错误的是( )

A.甲的速度是70米/分B.乙的速度是60米/分
C.甲距离景点2100米D.乙距离景点420米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com