
【题目】在Rt△ABO中,∠AOB=90°,OA=![]() ,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
,OB=4,分别以OA、OB边所在的直线建立平面直角坐标系,D为x轴正半轴上一点,以OD为一边在第一象限内作等边△ODE.
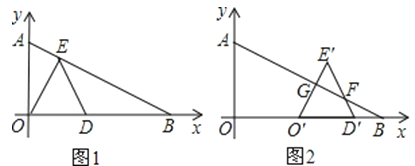
(1)如图①,当E点恰好落在线段AB上时,求E点坐标;
(2)在(Ⅰ)问的条件下,将△ODE沿x轴的正半轴向右平移得到△O′D′E′,O′E′、D′E′分别交AB于点G、F(如图②)求证OO′=E′F;
(3)若点D沿x轴正半轴向右移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式.
【答案】(1)E(1,![]() );(2)证明见解析;(3)见解析.
);(2)证明见解析;(3)见解析.
【解析】(1)由题意作辅助线,作EH⊥OB于点H,由BO=4,求得OE,然后求出OH,EH,从而得出点E的坐标;
(2)假设存在,由OO′=4-2-DB,而DF=DB,从而得到OO′=EF;
(3)根据题意分三种情况写出解析式即可.
(1)作EH⊥OB于点H,
tan∠ABO=![]() =
=![]() =
=![]() ,
,
∴∠ABO=30°,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=![]() OB=2.
OB=2.
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=![]() .
.
∴E(1,![]() );
);
(2)∵∠ABO=30°,∠EDO=60°,
∴∠ABO=∠DFB=30°,
∴D′F=D′B.
∴OO′=4﹣2﹣D′B=2﹣D′B=2﹣D′F=E′D′﹣FD′=E′F;
(3)当0<x≤2时,△ODE与△AOB重叠部分的面积为△ODE面积=![]() x2,
x2,
当2<x<4时,△ODE与△AOB重叠部分的面积为四边形GO′DF面积=﹣![]() x2+2
x2+2![]() x﹣2
x﹣2![]() ,
,
当x≥4时,△ODE与△AOB重叠部分的面积为2![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
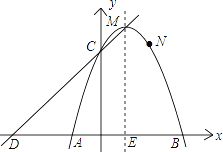
(1)求这个二次函数的解析式,并写出顶点M及点C的坐标;
(2)若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
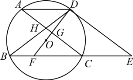
【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及其延长线分别交AC,BC于点G,F.
(1)求证:DF垂直平分AC;
(2)若弦AD=10,AC=16,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
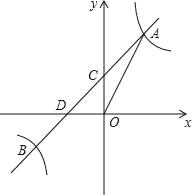
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)对于反比例函数y=![]() ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;
(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:EF∥AD,∠1=∠2,∠B=55°,求∠BDG的大小.
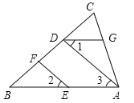
请同学们在下面的横线上把解答过程补充完整:
解:∵ EF//AD, (已知)
∴ ∠2=∠3, ( )
又∵ ∠1=∠2, (已知)
∴ ∠1=∠3, (等量代换)
∴ ,(内错角相等,两直线平行)
∴ ∠B+∠BDG=180°, ( )
∵ ∠B=55°, (已知)
∴ ∠BDG = .
查看答案和解析>>
科目:初中数学 来源: 题型:
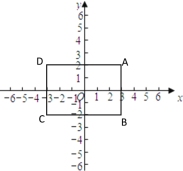
【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且![]() .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.
(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D是△ABC内一点,那么,在下列结论中错误的是( ).
A. BD+CD>BCB. ∠BDC>∠AC. BD>CDD. AB+AC>BD+CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,则阴影部分面积是_____
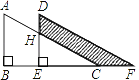
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com