
分析 (1)根据绝对值、零指数幂、特殊角的三角函数可以解答本题;
(2)先对括号内的式子通分,然后根据分式的除法进行化简即可.
解答 解:(1)|-1|-$\frac{1}{2}$×$\sqrt{8}$-(5-π)0+4cos45°
=1-$\frac{1}{2}×2\sqrt{2}$-1+4×$\frac{\sqrt{2}}{2}$
=1-$\sqrt{2}$-1+$2\sqrt{2}$
=$\sqrt{2}$;
(2)($\frac{{a}^{2}}{a+1}$-a+1)÷$\frac{a}{{a}^{2}-1}$
=$\frac{{a}^{2}-(a-1)(a+1)}{a+1}×\frac{(a+1)(a-1)}{a}$
=$\frac{{a}^{2}-{a}^{2}+1}{a+1}×\frac{(a+1)(a-1)}{a}$
=$\frac{1}{a+1}×\frac{(a+1)(a-1)}{a}$
=$\frac{a-1}{a}$.
点评 本题考查实数的混合运算、分式的混合运算、零指数幂、特殊角的三角函数、去绝对值,解题的关键是明确它们各自的计算方法.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )
如图,已知一次函数y=-x+2$\sqrt{2}$的图象与坐标轴分别交于A、B两点,⊙O的半径为1,P是线段AB上的一个点,过点P作⊙O的切线PM,切点为M,则PM的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
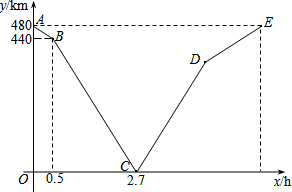 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系.根据图象解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com