
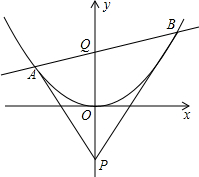
 已知抛物线y=ax2,点P、Q为抛物线对称轴上两点,且P、Q关于抛物线顶点对称,过Q点任意作一条直线与抛物线交于A、B两点,求证:抛物线对称轴平分∠APB.
已知抛物线y=ax2,点P、Q为抛物线对称轴上两点,且P、Q关于抛物线顶点对称,过Q点任意作一条直线与抛物线交于A、B两点,求证:抛物线对称轴平分∠APB. 分析 过点A作AM⊥y轴于M,过点B作BN⊥y轴于N,如图,设点A(x1,y1)、点B(x2,y2)、点Q(0,c),易得点P的坐标为(0,-c),设过点Q的直线为y=kx+c,则y1=kx1+c,y2=kx2+c,且x1和x2是ax2=kx+c即ax2-kx-c=0的两根,根据根与系数的关系可得x1+x2=$\frac{k}{a}$,x1•x2=-$\frac{c}{a}$,要证抛物线对称轴平分∠APB(即证∠NPB=∠APM),只需证tan∠NPB=tan∠APM即可.
解答 证明:过点A作AM⊥y轴于M,过点B作BN⊥y轴于N,如图.
设点A(x1,y1)、点B(x2,y2)、点Q(0,C),
则有AM=-x1,BN=x2.
设过点Q的直线为y=kx+c,
则y1=kx1+c,y2=kx2+c,
且x1和x2是ax2=kx+c即ax2-kx-c=0的两根,
∴x1+x2=-$\frac{-k}{a}$=$\frac{k}{a}$,x1•x2=-$\frac{c}{a}$
∵y=ax2的顶点为(0,0),P、Q关于抛物线顶点对称,
∴点P为(0,-c),
∴MP=y1-(-c)=y1+c=kx1+c+c=kx1+2c,
NP=y2-(-c)=y2+c=kx2+c+c=kx2+2c,
∴tan∠APM=$\frac{AM}{MP}$=$\frac{-{x}_{1}}{k{x}_{1}+2c}$,
tan∠NPB=$\frac{BN}{NP}$=$\frac{{x}_{2}}{k{x}_{2}+2c}$,
∴tan∠NPB-tan∠APM
=$\frac{{x}_{2}}{k{x}_{2}+2c}$-$\frac{-{x}_{1}}{k{x}_{1}+2c}$
=$\frac{{x}_{2}(k{x}_{1}+2c)+{x}_{1}(k{x}_{2}+2c)}{(k{x}_{2}+2c)(k{x}_{1}+2c)}$
=$\frac{2k{x}_{1}•{x}_{2}+2c({x}_{1}+{x}_{2})}{(k{x}_{1}+c)(k{x}_{2}+c)}$
=$\frac{2k•(-\frac{c}{a})+2c•\frac{k}{a}}{(k{x}_{1}+c)(k{x}_{2}+c)}$
=0,
∴tan∠NPB=tan∠APM,
∴∠NPB=∠APM,
∴PQ平分∠APB,
∴该抛物线对称轴平分∠APB.
点评 本题主要考查了抛物线的性质、直线与抛物线的交点问题、三角函数、根与系数的关系等知识,是一道通过代数推理解决几何问题的好题,运用作差法证到tan∠NPB=tan∠APM是解决本题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
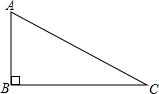 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
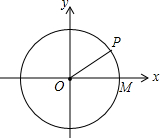 在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com