
分析 (1)首先化简二次根式,进而利用二次根式乘法运算法则得出答案;
(2)首先利用负整数指数幂的性质以及零指数幂的性质化简,再利用二次根式乘法运算法则得出答案.
解答 解:(1)(2$\sqrt{\frac{3}{2}}$-$\sqrt{\frac{1}{2}}$)×($\frac{1}{2}$$\sqrt{8}$+$\sqrt{\frac{2}{3}}$)
=(2×$\frac{\sqrt{6}}{2}$-$\frac{\sqrt{2}}{2}$)×($\frac{1}{2}$×2$\sqrt{2}$+$\frac{\sqrt{6}}{3}$)
=($\sqrt{6}$-$\frac{\sqrt{2}}{2}$)×($\sqrt{2}$+$\frac{\sqrt{6}}{3}$)
=2$\sqrt{3}$+2-1-$\frac{\sqrt{3}}{3}$
=$\frac{5\sqrt{3}}{3}$+1;
(2)(-$\sqrt{3}$)0+($\frac{1}{3}$)-1+$\sqrt{27}$-$\frac{2+\sqrt{3}}{2-\sqrt{3}}$
=1+3-3$\sqrt{3}$-(2+$\sqrt{3}$)2
=4-3$\sqrt{3}$-(7+4$\sqrt{3}$)
=-3-7$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
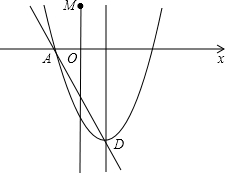 如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.
如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+3的图象经过点(3,0).
已知二次函数y=x2+bx+3的图象经过点(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com