
【题目】如图,五边形![]() 内接于
内接于![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
(1)若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由圆心角、弧、弦之间的关系得出![]() ,由圆周角定理得出∠ADE=∠DBC,证明△ADE≌△DBC,即可得出结论;
,由圆周角定理得出∠ADE=∠DBC,证明△ADE≌△DBC,即可得出结论;
(2)连接CO并延长交AB于G,作OH⊥AB于H,则∠OHG=∠OHB=90°,由切线的性质得出∠FCG=90°,得出△CFG、△OGH是等腰直角三角形,得出CF=CG,OG=![]() OH,由等边三角形的性质得出∠OBH=30°,由直角三角形的性质得出OH=
OH,由等边三角形的性质得出∠OBH=30°,由直角三角形的性质得出OH=![]() OB=1,OG=
OB=1,OG=![]() ,即可得出答案.
,即可得出答案.
(1)证明:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,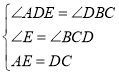 ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:连接![]() 并延长交
并延长交![]() 于
于![]() ,作
,作![]() 于
于![]() ,如图所示:
,如图所示:
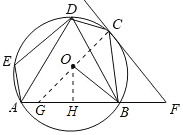
则![]() ,
,
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 、
、![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
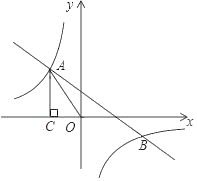
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的点
的图象交于第二、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 取得最大值时,求出点
取得最大值时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
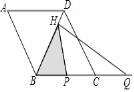
【题目】如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动并且始终保持BP=CQ,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为s,则能反映s与x之间的函数关系的图象大致为 ( )
A.  B.
B. 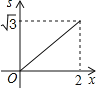 C.
C. 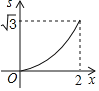 D.
D. 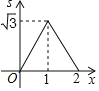
查看答案和解析>>
科目:初中数学 来源: 题型:
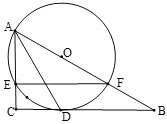
【题目】如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 经过点
经过点![]() ,与
,与![]() 相交于点E,与
相交于点E,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(I).如图,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
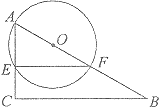
(II)如图,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() .
.
①求证:![]() 为
为![]() 的切线;
的切线;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
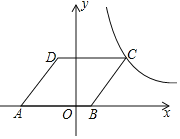
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( )
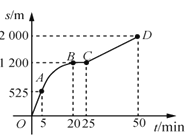
A.25min~50min,王阿姨步行的路程为800m
B.线段CD的函数解析式为![]()
C.5min~20min,王阿姨步行速度由慢到快
D.曲线段AB的函数解析式为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要在一块长52m,宽48m的矩形绿地上,修建同样宽的两条互相垂直的甬路.下面分别是小亮和小颖的设计方案.
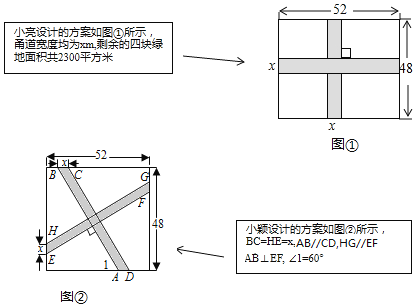
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积(友情提示:小颖设计方案中的与小亮设计方案中的取值相同)
查看答案和解析>>
科目:初中数学 来源: 题型:
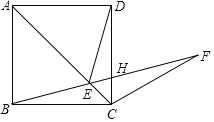
【题目】如图,在正方形ABCD的对角线AC上取一点E.使得![]() ,连接BE并延长BE到F,使
,连接BE并延长BE到F,使![]() ,BF与CD相交于点H,若
,BF与CD相交于点H,若![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则其中正确的结论有( )
.则其中正确的结论有( )
A. ①②③B. ①②③④C. ①②④D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com