
分析 (1)根据x、y的值可以求得x+y的值和xy的值,从而可以解答本题;
(2)根据x、y的值可以求得x+y的值和xy的值,从而可以解答本题.
解答 解:(1)∵x=$\frac{\sqrt{7}+\sqrt{5}}{2}$,y=$\frac{\sqrt{7}-\sqrt{5}}{2}$,
∴x+y=$\sqrt{7}$,xy=$\frac{1}{2}$,
∴x2-xy+y2
=(x+y)2-3xy
=$(\sqrt{7})^{2}-3×\frac{1}{2}$
=7-1.5
=5.5;
(2))∵x=$\frac{\sqrt{7}+\sqrt{5}}{2}$,y=$\frac{\sqrt{7}-\sqrt{5}}{2}$,
∴x+y=$\sqrt{7}$,xy=$\frac{1}{2}$,
∴$\frac{y}{x}$+$\frac{x}{y}$
=$\frac{{y}^{2}+{x}^{2}}{xy}$
=$\frac{(x+y)^{2}-2xy}{xy}$
=$\frac{(\sqrt{7})^{2}-2×\frac{1}{2}}{\frac{1}{2}}$
=12.
点评 本题考查分式的化简求值,解题的关键是明确分式的化简求值的方法.


科目:初中数学 来源: 题型:解答题
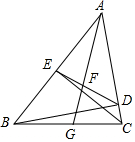 在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D,E,联结ED,∠BAC的平分线交ED于点F,交BC于点G,求证:AF:AG=ED:BC.
在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D,E,联结ED,∠BAC的平分线交ED于点F,交BC于点G,求证:AF:AG=ED:BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
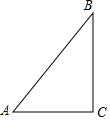 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD为中线,tanB=$\frac{1}{2}$,sinA=$\frac{3}{5}$,CA=10,求cos∠ADC的值.
如图,在△ABC中,CD为中线,tanB=$\frac{1}{2}$,sinA=$\frac{3}{5}$,CA=10,求cos∠ADC的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com