
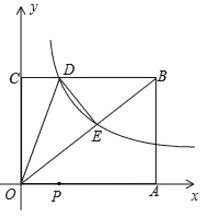
【题目】如图,已知矩形![]() 的两边OA,OC分别落在
的两边OA,OC分别落在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() 的中点E,且与BC边相交于点D.
的中点E,且与BC边相交于点D.
(1)①求反比例函数的解析式及点D的坐标;
②直接写出![]() 的面积为________.
的面积为________.
(2)若P是OA上的动点,当![]() 值为最小时,求直线
值为最小时,求直线![]() 的解析式.
的解析式.
【答案】(1)①反比例函数的解析式为![]() ;点D坐标为
;点D坐标为![]() ;②
;②![]() ;(2)直线PE的解析式为
;(2)直线PE的解析式为![]() .
.
【解析】
(1)①由E是OB的中点,即可求得E的坐标,利用待定系数法求得函数的解析式,进而求得D的坐标;
②根据S△ODE=S△OBC-S△OCD-S△BDE即可求解;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,
,![]() 与
与![]() 轴的交点P即为所求.利用待定系数法即可求出解析式.
轴的交点P即为所求.利用待定系数法即可求出解析式.
(1)①∵E是OB的中点,顶点B的坐标是![]() ,
,
∴E点坐标为![]() .
.
将点![]() 代入
代入![]() 中,得
中,得![]() .
.
∴反比例函数的解析式为![]() .
.
令![]() ,则
,则![]() ,
,
∴点D坐标为![]() .
.
②S△OBC=![]() BCOC=
BCOC=![]() ×6×4=12,
×6×4=12,
S△OCD=![]() OCCD=
OCCD=![]() ×4×img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/02/023f94ae/SYS202007220205239681262012_DA/SYS202007220205239681262012_DA.017.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />=3,
×4×img src="http://thumb.zyjl.cn/questionBank/Upload/2020/07/22/02/023f94ae/SYS202007220205239681262012_DA/SYS202007220205239681262012_DA.017.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />=3,
S△BDE=![]() ×(
×(![]() )×2=
)×2=![]() ,
,
则S△ODE=S△OBC-S△OCD-S△BDE=12-3-3-4.5=![]() .
.
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() .
.
连接![]() ,
,![]() 与
与![]() 轴的交点P即为所求.
轴的交点P即为所求.
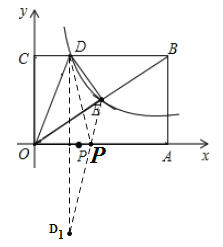
设直线PE解析式为![]() ,依题意得
,依题意得
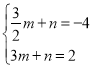 ,解得
,解得![]()
∴直线PE的解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
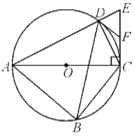
(1)求证:DF是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
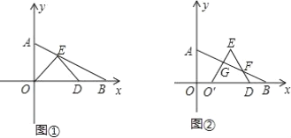
【题目】如图,在Rt△AOB中,∠ABO=30°,BO=4,分别以OA、OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内作等边△ODE.
(1)如图①当E点恰好落在线段AB上时,求E点坐标;
(2)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,当E点到达△AOB的外面,且点D在点B左侧时,写出y与x的函数关系式,并写出自变量x的取值范围;
(3)在(1)问的条件下,将△ODE在线段OB上向右平移如图②,图中是否存在一条与线段OO′始终相等的线段?如果存在,请直接指出这条线段;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
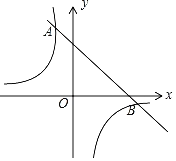
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足k1x+b>![]() 的x的取值范围.
的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(概念感知)
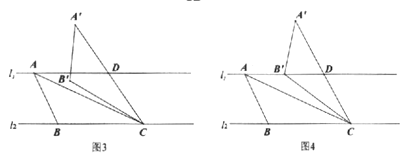
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否是“准黄金”三角形,请说明理由.
是否是“准黄金”三角形,请说明理由.

(问题探究)
(2)如图2,![]() 是“准黄金”三角形,BC是“金底”,把
是“准黄金”三角形,BC是“金底”,把![]() 沿BC翻折得到
沿BC翻折得到![]() ,连AB接AD交BC的延长线于点E,若点C恰好是
,连AB接AD交BC的延长线于点E,若点C恰好是![]() 的重心,求
的重心,求![]() 的值.
的值.
(拓展提升)
(3)如图3,![]() ,且直线
,且直线![]() 与
与![]() 之间的距离为3,“准黄金”
之间的距离为3,“准黄金”![]() 的“金底”BC在直线
的“金底”BC在直线![]() 上,点A在直线
上,点A在直线![]() 上.
上.![]() ,若
,若![]() 是钝角,将
是钝角,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,线段
,线段![]() 交
交![]() 于点D.
于点D.
①当![]() 时,则
时,则![]() _________;
_________;
②如图4,当点B落在直线![]() 上时,求
上时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,它的出现标志中国古代数学形成了完整的体系.其中有一个问题:“今有二马、一牛价过-万,如半马之价:一马、二牛价不满一万,如半牛之价.问牛、马价各几何?”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱:一匹马加上两头牛的价钱则不到一万,不足的部分正好是半头牛的价钱.问一头牛、一匹马各多少钱?设一匹马值![]() 钱、一头牛值
钱、一头牛值![]() 钱,则符合题意的方程组为( )
钱,则符合题意的方程组为( )
A. B.
B.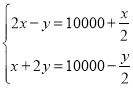
C.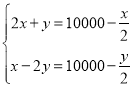 D.
D.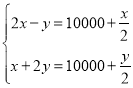
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某微商销售的某商品每袋成本20元,设销售价格为x(单位:元/袋),该微商发现销售量y与销售价格x之间的关系如表:
销售价格x(元/袋) | 25 | 30 | 35 | 40 |
销售件数y | 275 | 250 | 225 | 200 |
(1)求y关于x的函数表达式;
(2)根据物价部门的规定,商品的利润率不能超过100%,该微商应该如何定价,才能使获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com