
【题目】如图,在![]() 中
中![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
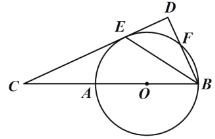
(1)求证:![]() .
.
(2)已知![]() 的半径为2,当
的半径为2,当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.元曲;D.论语.比赛形式分“单人组”和“双人组”.
(1)小明参加“单人组”,他从中随机抽取一个比赛项目,则抽到“唐诗”的是 事件,其概率是 ;
(2)若小亮和小丽组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小亮和小丽都没有抽到“元曲”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
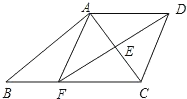
【题目】如图,已知:梯形ABCD中,AD∥BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.
(1)求证:AD=CF;
(2)在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)为弘扬 “东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…,按照此规律,第n个图中正方形和等边三角形的个数之和为( )个.

A.9nB.6nC.9n+3D.6n+3
查看答案和解析>>
科目:初中数学 来源: 题型:
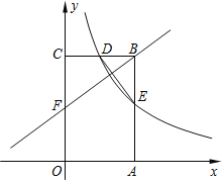
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为![]() .双曲线
.双曲线![]() 的图象经过BC的中点D,且与AB交于点E,连接DE.
的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
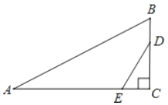
【题目】在Rt△ABC中,∠C=90°,AC=8,BC=6,点D、E分别在BC、AC上,且BD=CE,设点C关于DE的对称点为F,若DF∥AB,则BD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相较于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PH·PC;④若AB=2,则S△BPD=![]() ;其中正确的是( )
;其中正确的是( )
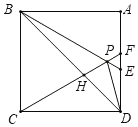
A.①②③④B.②③C.①②④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com