
【题目】已知直线 y13x 6与 x 轴、y 轴分别交于点 A,C;过点 C 的直线 y2x b 与 x 轴交于点 B.
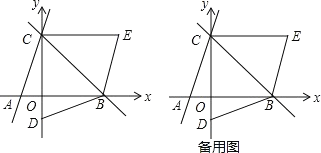
(1)b 的值为 ;
(2)若点 D 的坐标为(0,﹣2),将△BCD 沿直线 BC 对折后,点 D 落到第一象限的点 E 处, 求证:四边形 ABEC 是平行四边形;
(3)在直线 BC 上是否存在点 P,使得以 P、A、D、B 为顶点的四边形是平行四边形? 如果存在,请求出点 P 的坐标;如果不存在,请说明理由.
【答案】(1) 6; (2)见解析; (3)存在,点P的坐标为(4,2)或(8,![]() )
)
【解析】
(1)先由点C在直线![]() 上,求出点C坐标,代入直线
上,求出点C坐标,代入直线![]() 中即可;
中即可;
(2)先求出∠OBC=∠OCB=45°,进而判断出CE∥AB,最后判断出CE=AB即可;
(3) ∠OAD=∠ODA=45![]() ,∠OBC=∠OCB=45°,判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可,利用两点之间的距离公式即可得出点P坐标.
,∠OBC=∠OCB=45°,判断出AD∥BC,使得以P、A、D、B为顶点的四边形是平行四边形,只要AD=PB即可,利用两点之间的距离公式即可得出点P坐标.
(1)∵直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点C,
轴交于点C,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(0,6),
∵直线![]() 过点C,
过点C,
将点C的坐标为(0,6)代入![]() ,
,
解得:![]() ,
,
故答案为:6;
(2)当![]() 时,直线BC的解析式为
时,直线BC的解析式为![]() ,
,
∵点C的坐标为(0,6),
∴OC=6,
令![]() 得,
得,![]() ,
,
∴点B的坐标为(6,0),
∴OB=6,
∴OB=OC=6,
∴∠OBC=∠OCB=45°,
由折叠的性质得:∠BCE=∠OCB=45°,CE=CD,
∴∠OBC=∠BCE=45![]() ,
,
∴CE∥AB,
由![]() ,令
,令![]() 得,
得,![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=2,
∴AB=OA+OB=2+6=8,
∵点D的坐标为(0,![]() ),
),
∴OD=2,
∴CE=CD=OC+OD=8,
∴CE=AB,
又∵CE∥AB,
∴四边形ABEC为平行四边形;
(3)存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
如图,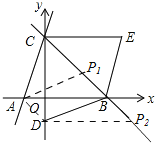
∵点A的坐标为(![]() ,0)、点D的坐标为(0,
,0)、点D的坐标为(0,![]() ),
),
∴OA=OD=2,
∴![]() ,∠OAD=∠ODA=45
,∠OAD=∠ODA=45![]() ,
,
由(2)得:∠OBC=∠BCE=45![]() ,
,
∴∠OBC=∠BCE=∠OAD=∠ODA=45![]() ,
,
∴AD∥BC,
∵直线BC解析式为![]() ,且点P在直线BC上,
,且点P在直线BC上,
∴设点P坐标为(![]() ,
,![]() ),
),
∴![]()
![]()
![]() ,
,
∵以P、A、D、B为顶点的四边形是平行四边形,
∴PB=AD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴P(4,2)或P(8,![]() ),
),
综上所述,存在点P,使以P、A、D、B为顶点的四边形是平行四边形.
点P的坐标为(4,2)或(8,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页0.8元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
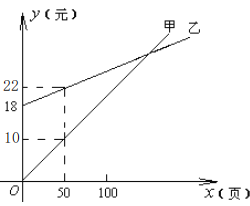
(1)乙复印社要求客户每月支付的承包费是_______元;
(2)当每月复印_______页时,两复印社实际收费相同;
(3)如果每月复印200页时,应选择_______复印社?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 30 | 160 | 1.1 |
草莓 | 15 | 50 | 1.6 |
(1)若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是大于1的实数,且有a3+a-3=p,a3-a-3=q.
(1)若p+q=4,求p-q的值;
(2)当q2=22n+![]() -2(n≥1,且n是整数)时,比较p与a3+
-2(n≥1,且n是整数)时,比较p与a3+![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个三角形的纸片ABC,其中∠A=∠C,
(1)把△ABC纸片按 (如图1) 所示折叠,使点A落在BC边上的点F处,DE是折痕.说明 BC∥DF;
(2)把△ABC纸片沿DE折叠,当点A落在四边形BCED内时 (如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
(3)当点A落在四边形BCED外时 (如图3),探索∠C与∠1、∠2之间的大小关系.(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.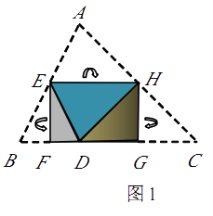
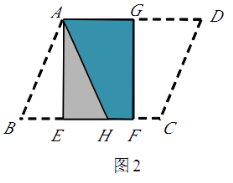

(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
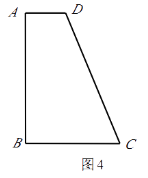
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com