
(1)试写出y与x之间的函数关系式(不必写出x的取值范围);
(2)试写出z与x之间的函数关系式(不必写出x的取值范围);
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价进行销售;第二年年获利不低于1130万元.请你借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
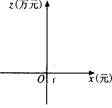
| 分析:由年获利=年销售额—生产成本—投资,可得z与x之间的函数关系式;根据函数图象来确定x的范围.
解:(1)依题意,知当销售单价定为x元时,年销售量减少 ∴ 即y与x之间的函数关系式是 ⑵由题意,得 即z与x之间的函数关系式是 ⑶∵ 当x取160时, ∴ 由根与系数的关系数,得过且过60+x=340,∴ x=180, 即同样的年获利,销售单价还可以定为180元. 当x=160时, ∴ 相应的年销售量分别为14万件和12万件. ⑷∵ ∴ 当x=170时,z取最大值,最大值为-310. 也就是说,当销售单价定为170元时,年获利最大,并且到第一年年底公司还差310万元就可收回全部投资. 第二年的销售单价定为x元时,则年获利为z=(30- 1510. 当z=1130时,即1130=-
由图象可以看出,当120≤x≤220时,z≥1130. 所以第二年的销售单价应确定在不低于120元且不高于220元的范围内. 点评:本题是一道经济决策性问题.要求学生能初步掌握一些有效地表示、处理数量关系的工具.能利用已有的生活经验从实际问题中建立数学模型,把所学知识应用到生活中去,解决身边的数学问题.并能从日常生活中提出简单的问题,会选择适当的方法解决问题,能表达解决问题的大致过程和结果.在复习过程中注意数学之间的联系,感受数学的整体性,不断丰富解决问题的策略,提高解决问题的能力.
|


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源:数学教研室 题型:013

A.0.36π平方米 B.0.811π平方米
C.2π平方米 D.3.24π平方米
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
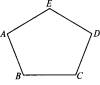
图1
(1)写出设计方案,并在图2中画出相应的图形;
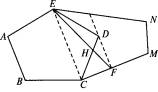
图2
(2)说明设计方案理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com