
分析 (1)根据乘法分配律进行变形,再计算即可;
(2)先去分母,移项,合并同类项,系数化成1即可;
(3)先去分母,移项,合并同类项,系数化成1即可;
(4)先去括号,再合并同类项,最后代入求出即可;
(5)①根据绝对值和偶次方的非负性求出即可;
②代入后展开,合并后即可求出答案.
解答 解:(1)-13×$\frac{2}{3}$-0.34×$\frac{2}{7}$+$\frac{1}{3}$×(-13)-$\frac{5}{7}$×0.34
=-13×($\frac{2}{3}$+$\frac{1}{3}$)-0.34×($\frac{2}{7}$+$\frac{5}{7}$)
=-13×1-0.34×1
=-13.34;
(2)$\frac{4x-3}{0.5}$-$\frac{5x-0.8}{0.2}$=$\frac{12-x}{0.1}$,
8x-6-25x+4=120-10x,
8x-25x+10x=120+6-4,
-7x=122,
x=-$\frac{122}{7}$;
(3)$\frac{x+3}{2}$-$\frac{13-3x}{6}$=1,
3(x+3)-(13-3x)=6,
3x+9-13+3x=6,
6x=10,
x=$\frac{5}{3}$;
(4)(2a-3b-ab)-(a-2b+3ab)
=2a-3b-ab-a+2b-3ab
=a-b-4ab,
当a-b=-1,ab=-2时,原式=-1-4×(-2)=7;
(5)①|a-1|+(ab-2)2=0,
a-1=0,ab-2=0,
a=1,ab=2,
a=1,b=2;
②$\frac{1}{ab}$+$\frac{1}{{({a+1})({b+1})}}$+$\frac{1}{{({a+2})({b+2})}}$+…+$\frac{1}{{({a+2004})({b+2004})}}$
=$\frac{1}{2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2005×2006}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2005}$-$\frac{1}{2006}$
=1-$\frac{1}{2006}$
=$\frac{2005}{2006}$.
点评 本题考查了整式的混合运算和求值、有理数的混合运算,解一元一次方程等知识点,能灵活运用知识点进行计算和化简是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
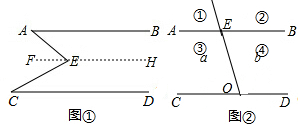 (1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.
(1)如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,EC.探究∠AEC,∠EAB,∠ECD之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40<x≤50 | B. | 40≤x<50 | C. | 40<x<50 | D. | 40≤x≤50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
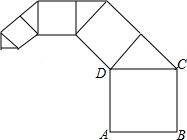 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com