
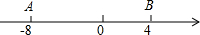 数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.
数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.分析 (1)设B点的运动速度为x,A、B两点同时出发相向而行,则他们的时间相等,列出等量关系:$\frac{8}{2}$=$\frac{4}{x}$,解得x即可;
(2)分两种情况,一种B在右侧,一种A点、B点重合;
(3)要想始终保持CA=2CB,则C点的速度应介于A、B两者之间,设出C点速度为x个单位/秒,联立方程,解方程即可得出结论.
解答 解:(1)设B点的运动速度为x,A、B两点同时出发相向而行,则他们的时间相等,
有:$\frac{8}{2}$=$\frac{4}{x}$,
解得x=1,
所以B点的运动速度为1个单位/秒;
(2)设t秒钟后,A、B与原点等距离.
∵OA+OB=8+4=12>6,且A点运动速度大于B点的速度,
∴分两种情况,
①当点B在点A的右侧时,8-2t=4+t,
解得t=$\frac{4}{3}$.
②当点A与点B的重合时,
2t=12+t,
解得t=12
综合①②得,$\frac{4}{3}$秒和12秒钟后,A、B与原点等距离.
(3)设点C的运动速度为x个单位/秒,运动时间为t,根据题意得知
8+(2-x)×t=[4+(x-1)×t]×2,
整理,得2-x=2x-2,
解得x=$\frac{3}{4}$.
故C点的运动速度为$\frac{3}{4}$个单位/秒.
∴CC1=$\frac{3}{4}$t,
∵A点的运动速度为2个单位/秒
∴AA1=2t,
∴$\frac{C{C}_{1}}{A{A}_{1}}$=$\frac{\frac{3}{4}t}{2t}$=$\frac{3}{8}$,
∴$\frac{C{C}_{1}}{A{A}_{1}}$的值不变.
点评 本题考查了一元一次方程的应用,难度较大,做题时要认真分析各个点的运动方向,找出等量关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | B. | 抛物线与y轴交于正半轴 | ||
| C. | 抛物线与x轴有两个交点 | D. | y有最大值,为-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
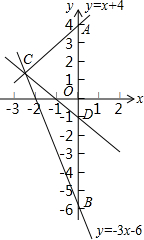 如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天一定不下雨 | |
| B. | 一个袋中装有5个红球,从中摸出一个是红球 | |
| C. | 购买1张彩票,中奖 | |
| D. | 随意翻到一本书的某项,这页的页码是奇数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com