
【题目】在△ABC中,AD平分∠BAC交BC于点D.
(1)在图1中,将△ABD沿BC的方向平移,使点D移至点C的位置,得到△A′B′D′,且A′B′交AC于点E,猜想∠B′EC与∠A′之间的关系,并说明理由; 
(2)在图2中,将△ABD沿AC的方向平移,使A′B′经过点D,得到△A′B′D′,求证:A′D′平分∠B′A′C. 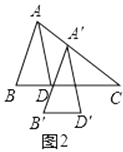
【答案】
(1)证:∠B′EC=2∠A′,其理由是:
∵△A′B′D′是由△ABD平移而来,
∴A′B′∥AB,∠A′=∠BAD.
∴∠B′EC=∠BAC.
∵AD平分∠BAC,
∴∠BAC=2∠BAD.
∴∠B′EC=2∠A′.
(2)证:∵△A′B′D′是由△ABD平移而来,
∴A′B′∥AB,∠B′A′D′=∠BAD.
∴∠B′A′C=∠BAC.
∵AD平分∠BAC,∴∠BAC=2∠BAD.
∴∠B′A′C═2∠B′A′D′.
∴A′D′平分∠B′A′C.
【解析】(1)根据平移的性质得到A′B′∥AB,∠A′=∠BAD,从而得到∠B′EC=∠BAC,然后根据AD平分∠BAC得到∠BAC=2∠BAD,从而得到∠B′EC=2∠A′;(2)根据平移的性质得到A′B′∥AB,∠B′A′D′=∠BAD,进一步得到∠B′A′C=∠BAC,然后根据AD平分∠BAC得到∠BAC=2∠BAD,从而得到∠B′A′C═2∠B′A′D′.
【考点精析】本题主要考查了平移的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】实数可分为正实数,零和__________.正实数又可分为__________和__________,负实数又可分为__________和__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】萧山北干初中组织外国教师(外教)进班上英语课,王明同学为了解全校学生对外教的喜爱程度,在全校随机抽取了若干名学生进行问卷调查.问卷将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型,根据调查结果绘制成了两幅不完整的统计图,请结合统计图信息解答下列问题:

(1)这次调查中,一共调查了 名学生,图1中C类所对应的圆心角度数为 ;
(2)请补全条形统计图;
(3)在非常喜欢外教的5位同学(三男两女)中任意抽取两位同学作为交换生,请用列表法或画树状图求出恰好抽到一名男生和一名女生作为交换生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4)
(1)求直线BD和抛物线对应的函数解析式;
(2)在抛物线对称轴上求一点P的坐标,使△ABP的周长最小;
(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M,O,N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图,现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系?
(3)连接CD、BD,则四边形ABDC的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com