
分析 连接AP.先根据三角形的面积公式分别表示出S△ABP,S△ACP,S△ABC,再由S△ABP=S△ACP+S△ABC即可得出PE=PF+PH,先根据直角三角形的性质得出AC=2CH,再由△ABC的面积为49,求出CH=7,由于CH>PF,则可分两种情况进行讨论:①P为底边BC上一点,运用结论PE+PF=CH,P为BC延长线上的点时,运用结论PE=PF+CH.
解答 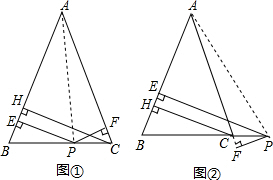 解:∵PE⊥AB,PF⊥AC,CH⊥AB,
解:∵PE⊥AB,PF⊥AC,CH⊥AB,
∴S△ABP=$\frac{1}{2}$AB•PE,S△ACP=$\frac{1}{2}$AC•PF,S△ABC=$\frac{1}{2}$AB•CH,
∵S△ABP=S△ACP+S△ABC,
∴$\frac{1}{2}$AB•PE=$\frac{1}{2}$AC•PF+$\frac{1}{2}$AB•CH,
又∵AB=AC,
∴PE=PF+CH,
∵在△ACH中,∠A=30°,
∴AC=2CH,
∵S△ABC=$\frac{1}{2}$AB•CH,AB=AC,
∴$\frac{1}{2}$×2CH•CH=49,
∴CH=7,
分两种情况:
①P为底边BC上一点,如图①.
∵PE+PF=CH,
∴PE=CH-PF=7-3=4;
②P为BC延长线上的点时,如图②.
∵PE=PF+CH,
∴PE=3+7=10.
故答案为:4或10.
点评 本题考查了等腰三角形的性质与三角形的面积,运用面积证明可使问题简便,分情况讨论是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA
如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.
如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com