
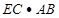 =4×60=240(m²)-------9分
=4×60=240(m²)-------9分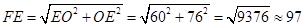 (m)-------13分
(m)-------13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
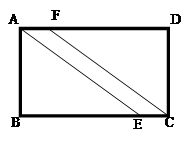
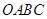 的直角顶点
的直角顶点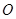 是坐标原点,边
是坐标原点,边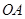 、
、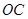 分别在
分别在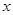 轴、
轴、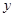 轴的正半轴上,
轴的正半轴上,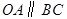 ,
,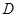 是
是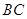 上一点,
上一点,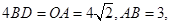
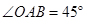 ,其中点
,其中点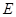 、
、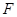 分别是线段
分别是线段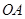 、
、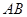 上的两个动点,且始终保持
上的两个动点,且始终保持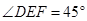 。
。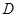 的坐标
的坐标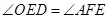 ;
;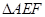 是等腰三角形时,△AEF关于直线EF的对称图形为
是等腰三角形时,△AEF关于直线EF的对称图形为 ,求
,求 与五边形OEFBC的重叠部分的面积.
与五边形OEFBC的重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 中,
中, ,半径为1的动圆⊙
,半径为1的动圆⊙ 从
从 点出发,以每秒3个单位的速度沿折线
点出发,以每秒3个单位的速度沿折线 向终点
向终点 移动,设移动的时间为秒;同时,⊙
移动,设移动的时间为秒;同时,⊙ 的半径
的半径 不断增大,且
不断增大,且 (≥0).(1)当
(≥0).(1)当 秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒.
秒时,两圆的位置关系是 ;(2)当t≥4秒时,若两圆外切,则t的值为 秒. 
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 第二次将纸片折叠使点
第二次将纸片折叠使点 与
与


 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 ,
, 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ,… .按上述方法折叠,
,… .按上述方法折叠, 交于点
交于点 ,则
,则 = ▲ ,
= ▲ , = ▲ .
= ▲ .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
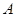 、
、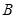 为直线
为直线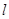 上两点,点
上两点,点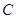 为直线
为直线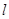 上方一动点,连接
上方一动点,连接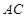 、
、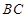 ,分别以
,分别以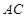 、
、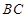 为边向
为边向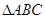 外作正方形
外作正方形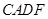 和正方形
和正方形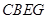 ,过点
,过点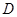 作
作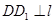 于点
于点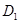 ,过点
,过点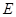 作
作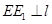 于点
于点 .
.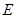 恰好在直线
恰好在直线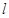 上时(此时
上时(此时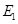 与
与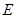 重合),试说明
重合),试说明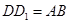 ;
;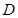 、
、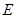 两点都在直线
两点都在直线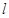 的上方时,试探求三条线段
的上方时,试探求三条线段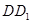 、
、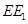 、
、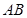 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;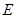 在直线
在直线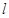 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段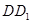 、
、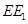 、
、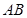 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)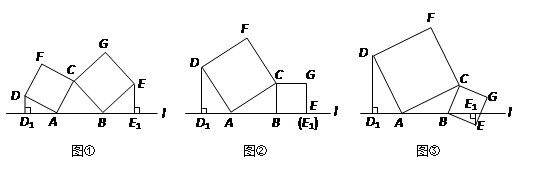
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com