
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

【答案】(1)y=-![]() x+3,M(2,2),N(4,1);
x+3,M(2,2),N(4,1);
(2)y=![]() ,点N在反比例函数图象上;
,点N在反比例函数图象上;
(3)3;
(4)k<0或0<k<4或k>8.
【解析】试题分析:(1)利用待定系数法即可求得直线DE的解析式,然后根据M的纵坐标是2,N的横坐标是4,即可求得M、N的坐标;
(2)利用待定系数即可求得反比例函数的解析式,然后把N的坐标代入解析式检验即可判断是否在反比例函数的图象上;
(3)根据△OMN的面积S=S梯形OCBM﹣S△OCN﹣S△BMN即可求解;
(4)根据经过M、N的反比例的函数的解析式,以及经过B的反比例函数的解析式,即可直接写出k的范围.
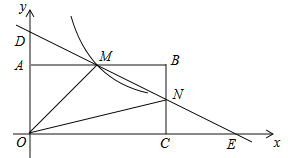
试题解析:解:(1)设直线DE的解析式是y=kx+b,根据题意得: ![]() ,解得:
,解得: 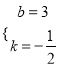 ,则直线DE的解析式是:y=﹣
,则直线DE的解析式是:y=﹣![]() x+3,令y=2,得到2=﹣
x+3,令y=2,得到2=﹣![]() x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
(2)把(2,2)代入![]() 得;k=4,则反比例函数的解析式是:
得;k=4,则反比例函数的解析式是: ![]() ,当x=4时,y=1,则N在
,当x=4时,y=1,则N在![]() 的图象上;
的图象上;
(3)S梯形OCBM=![]() (BM+OC)BC=
(BM+OC)BC=![]() (2+4)2=6,S△OCN=
(2+4)2=6,S△OCN=![]() OCCN=
OCCN=![]() ×4×1=2,S△BMN=
×4×1=2,S△BMN=![]() BNBM=
BNBM=![]() ×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
(4)经过M的反比例函数的解析式是: ![]() ,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
经过点B的反比例函数的解析式是: ![]() ,则当k>8时,函数与△BMN没有交点;
,则当k>8时,函数与△BMN没有交点;
当k<0时,函数图象在二、四象限,则与△BMN没有交点.
故k的范围是:0<k<4或k>8或k<0.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】现定义一种新运算:“※”,使得a※b=4ab
(1)求4※7的值;
(2)求x※x+2※x﹣2※4=0中x的值;
(3)不论x是什么数,总有a※x=x,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球试验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:

(1)请估计:当n很大时,摸到白球的概率约为______;(精确到0.1)
(2)估算盒子里有白球________个;
(3)若向盒子里再放入x个除颜色以外其他完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,请推测x的值最有可能是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y1=-![]() x与反比例函数y2=
x与反比例函数y2=![]() 的图象经过A(-2,1)点,求:
的图象经过A(-2,1)点,求:
(1)反比例函数的解析式.
(2)正比例与反比例函数另一个交点B的坐标.
(3)当x在什么范围,y1=y2,当x在什么范围,y1<y2,当x在什么范围,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
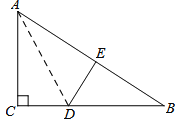
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
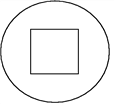
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D、E、F、G四点在△ABC的三边上,其中DG与EF相交于点H.若 ∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是( )
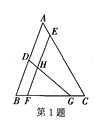
A.△BDG,△CEF B.△ABC,△CEF C.△ABC,△BDG D.△FGH,△ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com