
分析 (1)观察一系列等式确定出第10个等式即可;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的拆项方法计算即可.
解答 解:(1)第10个算式是$\frac{1}{10×11}$=$\frac{1}{10}$-$\frac{1}{11}$;
(2)第n个算式为$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(3)①1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$
=1+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=2-$\frac{1}{2015}$
=1$\frac{2014}{2015}$;
②$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$+$\frac{1}{32}$+$\frac{1}{42}$+$\frac{1}{56}$+$\frac{1}{72}$
=•1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{8}$-$\frac{1}{9}$
=1-$\frac{1}{9}$
=$\frac{8}{9}$;
③$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{101×103}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{101}$-$\frac{1}{103}$)
=$\frac{1}{2}$×(1-$\frac{1}{103}$)
=$\frac{51}{103}$;
④$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{97×100}$
=$\frac{1}{3}$×(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$…+$\frac{1}{97}$-$\frac{1}{100}$)
=$\frac{1}{3}$×(1-$\frac{1}{100}$)
=$\frac{33}{100}$.
点评 此题考查有理数的混合运算,掌握拆分的方法是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
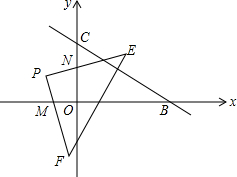 如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.
如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
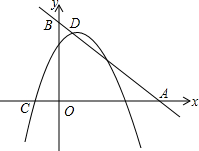 如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com