
|
 公司确定国内、国外市场的销量各为多少万辆时,该公司的年利润最大?
公司确定国内、国外市场的销量各为多少万辆时,该公司的年利润最大?
|
|
|
|
|
|
|


科目:初中数学 来源: 题型:
 (2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )
(2012•黄冈模拟)如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中错误的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
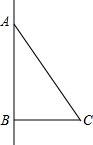 (2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是
(2012•黄冈模拟)如图,Rt△ABC的两直角边AB=4cm,BC=3cm.以AB所在直线为轴,将△ABC旋转一周后所得几何体的侧面展开图的面积是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com