
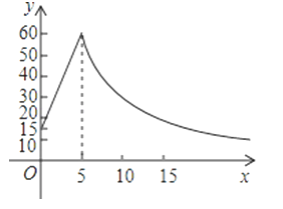
����Ŀ����ͼ��ʾ������һ�ֲ�Ʒ��ͬʱ����Ҫ��ԭ���ϼ��ȣ���ò����¶�Ϊy�棬�Ӽ��ȿ�ʼ�����ʱ��Ϊx���ӣ����˽⣬�ò����ڼ��ȹ������¶�y��ʱ��x��һ�κ�����ϵ����֪�ò����ڼ���ǰ���¶�Ϊ15�棬����5����ʹ�����¶ȴﵽ60��ʱֹͣ���ȣ�ֹͣ���Ⱥ����¶����½�����ʱ�¶�y��ʱ��x�ɷ�����������ϵ��
��1���ֱ�����ò��ϼ��ȹ����к�ֹͣ���Ⱥ�y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
��2�����ݹ���Ҫ���ڲ����¶Ȳ�����30������ʱ���ڣ���Ҫ�Ըò��Ͻ������������ô�Ըò��Ͻ�����������õ�ʱ���Ƕ��٣�
���𰸡���1��y=9x+15��0��x��5����y=![]() ��x��5������2��
��x��5������2��![]() ���ӣ�
���ӣ�
��������
��1��ȷ�������������ҵ�����ͼ���ĵ�����꣬�ô���ϵ������ú����Ľ���ʽ���ɣ�
��2���ֱ������������ĺ���ֵΪ30���������x��ֵ������ɵõ��𰸣�
��1������ȹ�����һ�κ�������ʽΪy=kx+b��k��0�����ú���ͼ���㣨0��15������5��60������![]() ����ã�
����ã�![]() ����һ�κ����ı���ʽΪy=9x+15��0��x��5���������ֹͣ������������ʽΪy
����һ�κ����ı���ʽΪy=9x+15��0��x��5���������ֹͣ������������ʽΪy![]() ��a��0�����ú���ͼ���㣨5��60������
��a��0�����ú���ͼ���㣨5��60������![]() 60����ã�a=300�����Է�������������ʽΪy
60����ã�a=300�����Է�������������ʽΪy![]() ��x��5����
��x��5����
��2��������ã�![]() ����ã�x1
����ã�x1 ����ã�x2=10����x2��x1=10
����ã�x2=10����x2��x1=10![]() �����ԶԸò��Ͻ�����������õ�ʱ��Ϊ
�����ԶԸò��Ͻ�����������õ�ʱ��Ϊ![]() ���ӣ�
���ӣ�


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ������A��-2,-8����
������A��-2,-8����
��1����������ߵĽ���ʽ��
��2���жϵ�B��-1��-4���Ƿ��ڴ��������ϣ�
��3�������������������Ϊ-6�ĵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ҵ���̨�Ϸ�����һ��ɹ�¼���ͼ��.ͼ����ɹ�¼ܵIJ���ʾ��ͼ������AB��CD�ཻ�ڵ�O��B��D�������ڵ��森��������AB��CD��136 cm��OA��OC��51 cm��OE��OF��34 cm���ֽ�ɹ�¼���ȫ�ȹ��ſ�������EF��һ���߶�����EF��32 cm.�������¼��ϵ�����ȹ�ܳ���С��________cmʱ������ȹ�Ų������䵽�����ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ֱ�ڵ���ĵ���AB��һ�ֽ�CD�̶���CD������45��нǣ���CDB=45�㣩����C���Ϸ�2�״��ӹ���һ������ED��ED������53��нǣ���EDB=53�㣩����ô����ED�ij���ԼΪ�����ף��������ȷ��1�ף��ο����ݣ�sin53���0.80��cos53���0.60��tan53���1.33��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣬�ں�����д����Ӧ�ĺ�����ϵʽ�����ж�y�Ƿ�Ϊx�ķ��������������������ں���Ŀո��ڴ���1���������������ں���Ŀո��ڴ���0������
��1�������ε����S��cm2��һ�������ij�y��cm�����x��cm��֮��Ĺ�ϵʽΪ��________ ��
��2�������εĶԽ��߳�y��cm�������ı߳�x��cm��֮��Ĺ�ϵʽΪ��________ ��
��3��һ����Ʒ�ĵ���Ϊa��Ԫ/�����������ѵ�Ǯ��y��Ԫ���빺��ļ���x�������Ĺ�ϵʽΪ��________ ��
��4��С���ļ���ѧУ���2400m���������г���ѧ���ٶ�v��m/s��������ʱ��t��s���Ĺ�ϵʽΪ��________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�ACΪֱ������B�ǻ�AC���е㣬��AC��7��BD��6�������ĸ�������ɵ���Ӱ���ֵ����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����O���P�ཻ��A��B���㣬��P�ڡ�O�ϣ���O����AC�С�P�ڵ�A��CP�����ӳ��߽���P��D��E������E��EF��CE��CB���ӳ�����F��
��1����֤��BC�ǡ�P�����ߣ�
��2����CD��2��CB��2![]() ����EF�ij���
����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�鳤���ξ��沣�������������������ܳ���ȵı߿��Ƴ�һ�澵�ӣ����ӵij�����ı���2��1����֪���沣���ļ۸���ÿƽ����120Ԫ���߿�ļ۸���ÿ��30Ԫ�������������澵�ӻ���ӹ���45Ԫ�����������澵�ӵ��ܷ�����![]() Ԫ�����ӵĿ���
Ԫ�����ӵĿ���![]() �ף�
�ף�
��1����![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��2������������澵�ӹ�����195Ԫ�������澵�ӵij��Ϳ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com