
 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.分析 (1)根据垂直定义得出∠AEB=∠BFC=90°,AB=BC,结合∠ABE=∠BCF,证明△ABE≌△BCF,可得AE=BF,于是AE2+CF2=BF2+CF2=BC2;
(2)设AP=x,则PD=4-x,由已知∠DPM=∠PAE=∠ABP,△PDM∽△BAP,列出关于x的一元二次函数,求出DM的最大值.
解答 (1)证明:∵AE⊥BP,CF⊥BP,
∴∠AEB=∠BFC=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
又∵∠ABE+∠FBC=∠BCF+∠FBC,
∴∠ABE=∠BCF,
∵在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠AEB=∠BFC}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴AE=BF,
∴AE2+CF2=BF2+CF2=BC2=42=16;
(2)解:设AP=x,则PD=4-x,
∵四边形ABCD是正方形,
∴∠D=∠BAP=90°,∠DCB=90°,
∴∠DPM+∠DMP=90°,∠DCF+∠BCF=90°,
∵PM∥CF,
∴∠DMP=∠DCF,
∴∠DPM=∠BCF,
由(1)知:∠BCF=∠ABP,
∴∠DPM=∠ABP,
∵∠D=∠BAP,
∠DPM=∠PAE=∠ABP,
∴△PDM∽△BAP,
∴$\frac{DM}{AP}$=$\frac{PD}{BA}$,
即$\frac{DM}{4-x}$=$\frac{x}{4}$,
∴DM=$\frac{x(4-x)}{4}$=-$\frac{1}{4}$x2+x,
当x=2时,即点P是AD的中点时,DM有最大值为1.
点评 本题主要考查正方形的性质等知识点,解答本题的关键是熟练掌握全等三角形的判定定理以及三角形相似等知识,此题有一定的难度,是一道不错的中考试题.


科目:初中数学 来源: 题型:解答题
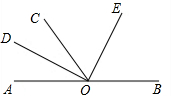 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com