练习册

  • 练习册
  • 试题
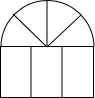    精英家教网 > 初中数学 > 题目详情
    如图所示，半圆的半径为AB，C为半圆周上一点．精英家教网
    （1）若∠CAB=30°，BC=6，求图中阴影部分的面积；
    （2）若AB=2R，则C运动到何处时，阴影部分的面积最小，最小面积是多少？
    分析：（1）阴影部分的面积即是半圆的面积-直角三角形的面积；
    （2）要使阴影部分的面积最小，则需直角三角形的面积最大，即斜边上的高最大，显然是到弧的中点时即可．
    解答：解：（1）∵∠CAB=30°，BC=6
    ∴AB=12
    ∴S半圆=π×36÷2=18π
    ∵∠CAB=30°，BC=6
    ∴AC=
    		122-62
    =6
    		3

    ∴S△ABC=6
    		3
    ×6×
    1
    2
    =18
    		3

    ∴S阴影=S半圆-S△ABC=18π-18
    		3
    ；

    （2）阴影部分的面积最小，则直角三角形的面积最大，
    即斜边上的高最大，
    ∴当CA=CB时，S最小值=
    1
    2
    πR2-R2．
    点评：注意：熟练运用锐角三角函数解直角三角形，求得各边的长，根据直角三角形和圆的面积公式进行计算．讨论面积的最值注意进行转换为容易分析的图形的面积．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网某建筑物的窗口如图所示，它的上半部是半圆，下半部是矩形，制造窗框的材料总长（图中所有黑线的长度和）为15m，当半圆的半径为多少时，窗户通过的光线最多？此时，窗户的面积是多少（结果精确到0.01m）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

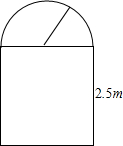    精英家教网一条隧道的截面如图所示，它的上部是一个半圆，下部是一个矩形，矩形的一边长为2.5m．
    （1）求隧道截面的面积S（m2）与上半部半径r（m）的函数关系式．
    （2）求当上部半圆半径为2m的截面面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，半圆的半径为AB，C为半圆周上一点．
    （1）若∠CAB=30°，BC=6，求图中阴影部分的面积；
    （2）若AB=2R，则C运动到何处时，阴影部分的面积最小，最小面积是多少？

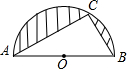
    查看答案和解析>>

    科目：初中数学 来源：《24.4 弧长和扇形面积》2009年同步练习（解析版） 题型：解答题

    如图所示，半圆的半径为AB，C为半圆周上一点．
    （1）若∠CAB=30°，BC=6，求图中阴影部分的面积；
    （2）若AB=2R，则C运动到何处时，阴影部分的面积最小，最小面积是多少？

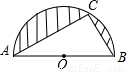
    查看答案和解析>>

    同步练习册答案