
分析 (1)根据题意首先表示出两种树苗的数量,再利用各种树苗的单价表示出总费用,进而得出答案;
(2)利用一次函数的增减性得出x的值进而得出答案.
解答 解:(1)设A种树苗x棵,则B种树苗(100-x)棵,
由题意可得:3x≤(100-x)≤4x,
解得:20≤x≤25,
则y=40x+80(100-x)
=-40x+8000;
(2)∵y=-40x+8000中,-40<0,
∴y随x的增大而减小,
∴x=25时,y将取到最小值,
故y=-40×25+8000=7000(元),
即A种树苗25棵,B种树苗75棵.
点评 此题主要考查了一元一次不等式的应用以及一次函数增减性等知识,正确利用一次函数增减性分析是解题关键.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:填空题
 星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法:
星晴天,小亮从家里骑自行车到同学家去玩,然后返回,如图是他离家的路程y(千米)与实际x(分钟)的函数图象,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
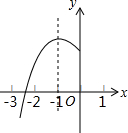 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图所示,则下列结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下题及其证明过程:
阅读下题及其证明过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com