
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,有下列结论:①
,其部分图象如图所示,有下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 增大而增大;④抛物线的顶点坐标为
增大而增大;④抛物线的顶点坐标为![]() ;⑤若方程
;⑤若方程![]() 两根为
两根为![]() (
(![]() ),则
),则![]() ,
,![]() .其中正确结论有( )
.其中正确结论有( )

A.1个B.2个C.3个D.4个
【答案】B
【解析】
由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结论①错误;当x=-1时,y>0,得到a-b+c>0,结论②错误;根据抛物线的对称性得到结论③错误;将x=2代入二次函数解析式中结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;根据抛物线![]() 的图象与直线
的图象与直线![]() 的交点情况判断⑤.
的交点情况判断⑤.
①∵抛物线![]() a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),
∴抛物线过原点,
∴![]() ,
,
∴![]() ,结论①错误;
,结论①错误;
②∵当x=-1时,y>0,
∴a-b+c>0,结论②错误;
③∵抛物线开口向上,
∴当x<2时,y随x增大而减小,③错误;
④抛物线![]() a≠0)的对称轴为直线x=2,且抛物线过原点,
a≠0)的对称轴为直线x=2,且抛物线过原点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴抛物线的顶点坐标为![]() ,结论④正确;
,结论④正确;
⑤∵抛物线与x轴的交点坐标为(4,0),(0,0),
∴抛物线的解析式也可以写作:![]() ,
,
方程![]() 两根
两根![]() ,可以看作是:抛物线
,可以看作是:抛物线![]() 与直线
与直线![]() 的两个交点的横坐标,
的两个交点的横坐标,
∴![]() ,结论⑤正确;
,结论⑤正确;
综上所述,正确的结论有:④⑤.
故选:B.


科目:初中数学 来源: 题型:
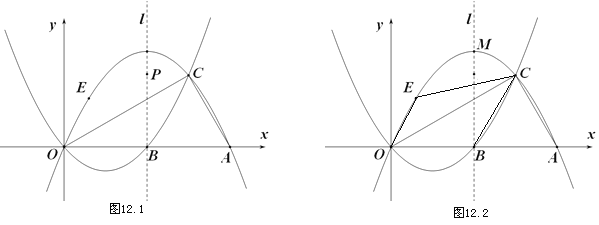
【题目】如图,抛物线![]() :
:![]() 与
与![]() :
:![]() 相交于点
相交于点![]() 、
、![]() ,
,![]() 与
与![]() 分别交
分别交![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() 为线段
为线段![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)抛物线![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() ,在(2)的条件下:
,在(2)的条件下:
①点![]() 为抛物线
为抛物线![]() 对称轴
对称轴![]() 上一动点,当
上一动点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标;
的坐标;
②如图12.2,点![]() 在抛物线
在抛物线![]() 上点
上点![]() 与点
与点![]() 之间运动,四边形
之间运动,四边形![]() 的面积是否存在最大值?若存在,求出面积的最大值和点
的面积是否存在最大值?若存在,求出面积的最大值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.
(1)求证:∠ABC=∠ABO;
(2)若AB=![]() ,AC=1,求⊙O的半径.
,AC=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若这个方程有实数根,求k的取值范围;
(2)若这个方程有一个根为1,求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现,该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数.其售价、周销售量、周销售利润
(元/件)的一次函数.其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)求![]() 关于
关于![]() 的函数解析式(不写出自变量的取值范围);
的函数解析式(不写出自变量的取值范围);
(2)该商品进价是 元/件;求售价是多少元/件时,周销售利润最大,最大利润是多少元?
(3)由于某种原因,该商品进价提高了![]() 元/件(
元/件(![]() ),物价部门规定该商品售价不得超过65元/件.该商店在今后的销售中,周销售量与售价仍然满足(1)中函数关系.若周销售最大利润是1400元,则
),物价部门规定该商品售价不得超过65元/件.该商店在今后的销售中,周销售量与售价仍然满足(1)中函数关系.若周销售最大利润是1400元,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
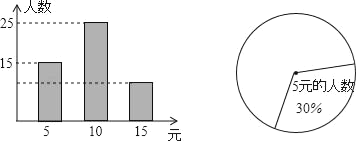
【题目】如图是某校九年级学生为灾区捐款情况抽样调查的条形图和扇形统计图.
(1)求抽样调查的人数;
(2)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数;
(3)若该校九年级学生有1000人,据此样本估计九年级捐款总数为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
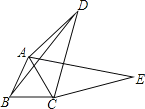
【题目】如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
(1)求证:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4![]() .求CD的长.
.求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com