
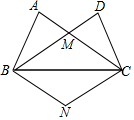
 如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.
如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M.分析 (1)由全等三角形的判定定理SSS证得结论;
(2)首先根据△ABC≌△DCB可得∠DBC=∠ACB,进而可得BM=CM,根据CN∥BD、BN∥AC,可判定四边形BNCM是平行四边形,再根据邻边相等的平行四边形是菱形可得结论.
解答  (1)证明:∵在△ABC和△DCB中,
(1)证明:∵在△ABC和△DCB中,
$\left\{\begin{array}{l}{AB=DC}\\{AC=DB}\\{BC=CB}\end{array}\right.$.
∴△ABC≌△DCB(SSS);
(2)∵△ABC≌△DCB,
∴∠DBC=∠ACB,
∴MB=MC.
∵CN∥BD,BN∥AC,
∴四边形BNCM为平行四边形.
又∵MB=MC,
∴平行四边形BNCM为菱形.
点评 此题主要考查了全等三角形的判定和性质,以及菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
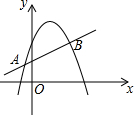 如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.
如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是x<-1或x>4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
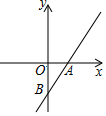 如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2).
如图,直线y=kx+b与x轴交于点A(1,0),与 y交于点B(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
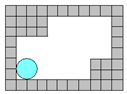 将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)
将半径为2cm的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的内侧滚动一周,回到开始位置后,圆心经过的路线的长度为 ( )(精确到0.01cm)| A. | 36cm | B. | 42.28cm | C. | 40.28cm | D. | 40cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com