
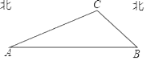
【题目】如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米.
(1)求农户c到公路B的距离;(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
(2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米?
【答案】(1)农户C到公路的距离![]() 米;(2)原计划该工程队毎天修路100米.
米;(2)原计划该工程队毎天修路100米.
【解析】
(1)农户C到公路的距离,也就是求C到AB的距离.要构造直角三角形,再解直角三角形;
(2)设原计划y天完成,则由等量关系“原工作效率×(1+25%)=提前完成时的工作效率”列方程求解.
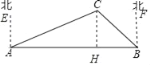
(1)如图,过C作CH⊥AB于H.
设CH=x,
由已知有∠EAC=68°,∠FBC=45°,
则∠CAH=22°,∠CBA=45°.
在Rt△BCH中,BH=CH=x,
在Rt△HAC中,tan∠HAC=![]() ,
,
∴HA=![]() ,
,
∵AH+HB=AB,
∴x+![]() x=2400,
x=2400,
解得x=![]() ,
,
∴农户C到公路的距离![]() 米.
米.
(2)设原计划完成这项工程需要y天,则实际完成工程需要(y﹣4)天.
根据题意得:![]() =(1+20%)×
=(1+20%)×![]() ,
,
解得:y=24.
经检验知:y=24是原方程的根,
2400÷24=100(米).
答:原计划该工程队毎天修路100米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
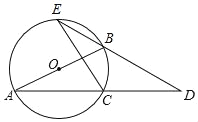
【题目】如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E.
(1)求证:CD=CE;
(2)连结AE,若∠D=25°,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等腰![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、点
、点![]() .
.
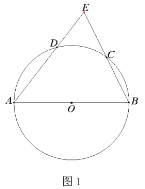
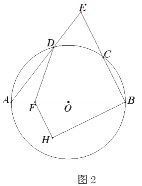
(1)如图1,求证:点![]() 为弧
为弧![]() 的中点;
的中点;
(2)如图2,点![]() 为直径
为直径![]() 上一点,过点
上一点,过点![]() 作
作![]() ,交过点
,交过点![]() 且垂直于
且垂直于![]() 的直线于点
的直线于点![]() ,连接
,连接![]() ,
,![]() ,设
,设![]()
![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
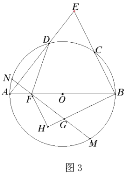
(3)如图3,在(2)的条件下,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]()
![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=α°,AB=AC,D是BC上一点,将AD绕点A顺时针旋转α°,得到线段AE,连接BE.
(1)(特例感知)如图1,若α=90,则BD+BE与AB的数量关系是 .
(2)(类比探究)如图2,若α=120,试探究BD+BE与AB的数量关系,并证明.
(3)(拓展延伸)如图3,若α=120,AB=AC=4,BD=![]() ,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
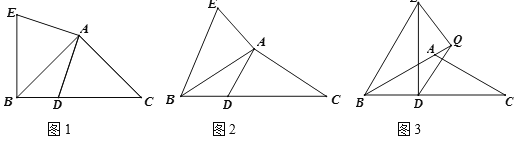
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B为反比例函数y=![]() 图象上的点,AD⊥x轴于点D,直线AB分别交x轴,y轴于点E,C,CO=OE=ED.
图象上的点,AD⊥x轴于点D,直线AB分别交x轴,y轴于点E,C,CO=OE=ED.
(1)求直线AB的函数解析式;
(2)F为点A关于原点的对称点,求△ABF的面积.
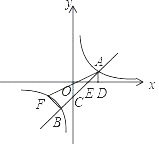
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.
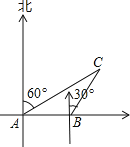
(1)试说明点B是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
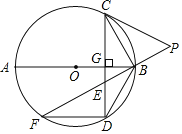
【题目】如图,AB为⊙O的直径,CD⊥AB于点G,E是CD上一点,且BE=DE,延长EB至点P,连接CP,使PC=PE,延长BE与⊙O交于点F,连结BD,FD.
(1)连结BC,求证:△BCD≌△DFB;
(2)求证:PC是⊙O的切线;
(3)若tanF=![]() ,AG﹣BG=
,AG﹣BG=![]() ,求ED的值.
,求ED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且![]() .
.
(1)求证:PD是⊙O的切线;
(2)若AD=12,AM=MC,求![]() 的值.
的值.
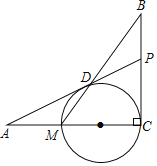
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
(3)在(2)的条件下,若要求生产A型号手写板的数量不能少于B型号手写板数量的2倍,请你设计出总获利最大的生产方案,并求出最大总获利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com