
【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.
(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使S△QAM= ![]() S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)证明:连接CM, 
∵AO是直径,M是圆心,
∴CM=OM,∠ACO=90°,
∴∠MOC=∠MCO.
∵D为OB的中点,
∴CD=OD,
∴∠DOC=∠DCO.
∵∠DOC+∠MOC=90°,
∴∠DCO+∠MCO=90°,
即∠MCD=90°,
∴CD是⊙M的切线
(2)解:方法一:
∵∠ACO=∠AOB=90°,∠OAB=∠OAB,
∴△ACO∽△AOB,
∴ ![]() ,
,
∴ ![]() ,
,
∴AB= ![]() .
.
在Rt△AOB中,由勾股定理,得
BO= ![]() ,
,
∵D为OB的中点,
∴OD= ![]() OB=
OB= ![]() ,
,
∴D(0, ![]() ).
).
∵OM=AM= ![]() OA=
OA= ![]() ,
,
∴M( ![]() ,0).设抛物线的解析式为y=a(x﹣
,0).设抛物线的解析式为y=a(x﹣ ![]() )(x﹣5),由题意,得
)(x﹣5),由题意,得
![]() =a(0﹣
=a(0﹣ ![]() )(0﹣5),
)(0﹣5),
解得:a= ![]() ,
,
∴抛物线的解析式为:y= ![]() (x﹣
(x﹣ ![]() )(x﹣5),
)(x﹣5),
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
连接AD交对称轴于P,设直线AD的解析式为y=kx+b,由题意,得
 ,
,
解得:  ,
,
∴直线AD的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
当x= ![]() 时,
时,
y= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
方法二:
∵OA=5,AC=3,∠ACO=90°,
∴OC=4,tan∠CAO= ![]() ,
,
∴OB= ![]() ,
,
∵D为BO的中点,
∴D(0, ![]() ),M(
),M( ![]() ,0),A(5,0),
,0),A(5,0),
∴设抛物线的解析式为:y=a(x﹣ ![]() )(x﹣5),
)(x﹣5),
把D(0, ![]() )代入得a=
)代入得a= ![]() ,
,
∴抛物线的解析式为:y= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∵P为对称轴上一点,
∴PM=PA,
∴△PDM的周长最小时,D,P,A三点共线,
∵D(0, ![]() ),A(5,0),
),A(5,0),
∴lAD:y=﹣ ![]() x+
x+ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() ,
,
∴P( ![]() ,
, ![]() ).
).
(3)解:存在.
∵S△PDM=S△ADM﹣S△APM,
∴S△PDM= ![]() ×
× ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() ,
,
= ![]() ,
,
∴S△QAM= ![]() =
= ![]() .
.
设Q的纵坐标为m,由题意,得
![]() ,
,
∴|m|= ![]() ,
,
∴m=± ![]() ,
,
当m= ![]() 时,
时,
![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
x1= ![]() ,x2=
,x2= ![]() ,
,
当m=﹣ ![]() 时,
时,
﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
x= ![]() .
.
∴Q( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ).
).
【解析】本题是一道二次函数与几何的综合题.解答此题的关键是求出抛物线的解析式.
(1)连接CM,由题意易得CM=OM,从而得到∠MOC=∠MCO,由OA为直径,根据圆周角的推论可得∠ACO=90°,易证CD=OD,∠DOC=∠DCO,由∠DOC+∠MOC=90°就可得∠DCO+∠MCO=90°,从而可得结论;
(2)根据已知条件可得△ACO∽△AOB求得AC:AO=AO:AB,从而求出AB,在Rt△AOB中由勾股定理求出OB的长,根据D是OB的中点可求得D的坐标,由待定系数法就可求得抛物线的解析式,从而求出其对称轴,连接AD交对称轴于P,先求出AD的解析式就可得点P的坐标;
(3)根据S△PDM=S△ADM-S△APM,可求得△PDM的面积,从而表示出△QAM面积的大小,设Q的纵坐标为m,根据三角形的面积可求出Q的横坐标,即可得
【考点精析】掌握圆周角定理和切线的判定定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是:( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
①分别以A,C为圆心,a为半径(a>![]() AC)作弧,两弧分别交于M,N两点;
AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.

(1)请在图中直线标出点F并连接CF;
(2)求证:四边形BCFD是平行四边形;
(3)当∠B为多少度时,四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民通行,某广场计划对坡角为30°,坡长为60米的斜坡AB进行改造,在斜坡中点D处挖去部分坡体(阴影表示),修建一个平行于水平线CA的平台DE和一条新的斜坡BE.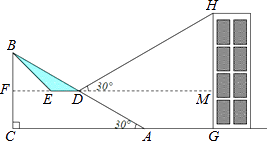
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}=![]() =
=![]() ;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=
;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=![]()
解决下列问题:
(1)若min{2,2x+2,4﹣2x}=2,则x的范围__________;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么__________(填a,b,c的大小关系)”.
③运用②的结论,若M{2x+y+2,x+2y,2x﹣y}=min{2x+y+2,x+2y,2x﹣y},求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
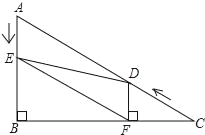
【题目】如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)DF= ;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com