
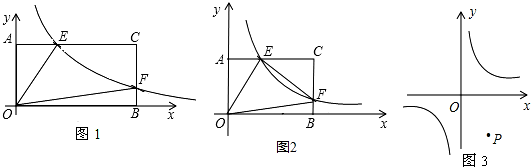
分析 (1)设OB=a,OA=b,用a、b表示出点E、F的坐标,再找出AE、EC、BF、CF,由此即可得出结论;
(2)①根据AE:EC=1:2,结合(1)结论以及所设未知数,可得出CE、CF的长,再结合△CEF的面积为4,即可求出ab值,从而可得出S△AOE的值,结合反比例函数系数k的几何意义即可得出结论;
②假设存在,分OP为边和OP为对角线来考虑.当OP为边时,设出点M的坐标,根据平行四边形的性质找出点N的坐标,再结合反比例函数图象上点的坐标特征即可求出点M的坐标;当OP为对角线时,设出点M、N的坐标,根据平行四边形的性质--对角线互相平分可求出点M的坐标.综上即可得出结论.
解答 解:(1)相等.理由如下:
设OB=a,OA=b,则E($\frac{k}{b}$,b),F(a,$\frac{k}{a}$),
∴AE=$\frac{k}{b}$,EC=a-$\frac{k}{b}$,BF=$\frac{k}{a}$,CF=b-$\frac{k}{a}$,
∴$\frac{AE}{EC}$=$\frac{\frac{k}{b}}{a-\frac{k}{b}}=\frac{k}{ab-k}$,$\frac{BF}{FC}$=$\frac{\frac{k}{a}}{b-\frac{k}{a}}$=$\frac{k}{ab-k}$,
∴$\frac{AE}{EC}$=$\frac{BF}{FC}$.
(2)①∵AE:EC=1:2,
∴BF:FC=1:2.
根据(1)所设,CE=$\frac{2}{3}$a,CF=$\frac{2}{3}$b,
∵S△CEF=$\frac{1}{2}$•CE•CF=$\frac{1}{2}$×$\frac{2}{3}$a×$\frac{2}{3}$b=4,
∴ab=18,
∴S△AOE=$\frac{1}{2}$×$\frac{1}{3}$a×b=$\frac{1}{6}$ab=3=$\frac{1}{2}$k,
∴k=6,
∴反比例函数的解析式为y=$\frac{6}{x}$.
②假设存在.
当OP是平行四边形的边时,如图4、5所示.
∵点O(0,0),点P(2,-2),
∴设点M(a,$\frac{6}{a}$),则点N(a+2,$\frac{6}{a}$-2),
∵点N在反比例函数y=$\frac{6}{x}$的图象上,
∴(a+2)×($\frac{6}{a}$-2)=6,
解得:a=-1-$\sqrt{7}$或a=-1+$\sqrt{7}$,
∴点M的坐标为(-1-$\sqrt{7}$,1-$\sqrt{7}$)或(-1+$\sqrt{7}$,1+$\sqrt{7}$);
当OP为对角线时,如图6所示.
设M(a,$\frac{6}{a}$),N(b,$\frac{6}{b}$),
∵OP的中点坐标为(1,-1),
∴有$\left\{\begin{array}{l}{a+b=2}\\{\frac{6}{a}+\frac{6}{b}=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1-\sqrt{7}}\\{b=1+\sqrt{7}}\end{array}\right.$或$\left\{\begin{array}{l}{a=1+\sqrt{7}}\\{b=1-\sqrt{7}}\end{array}\right.$(舍去),
∴点M的坐标为(1-$\sqrt{7}$,-1-$\sqrt{7}$).
综上可知:在反比例函数y=$\frac{k}{x}$的图象上存在点M、N(M在N的左侧),使得以O、P、M、N为顶点的四边形是平行四边形,点M的坐标为(-1-$\sqrt{7}$,1-$\sqrt{7}$)、(-1+$\sqrt{7}$,1+$\sqrt{7}$)或(1-$\sqrt{7}$,-1-$\sqrt{7}$).
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数系数k的结合意义以及平行四边形的性质,解题的关键是:(1)利用含a、b的代数式表示出来AE、EC、BF、CF;(2)①求出ab值;②分情况讨论.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的性质结合已知两点的坐标找出另外两点坐标间的关系是关键.


科目:初中数学 来源: 题型:选择题
| A. | 平均数是2 | B. | 众数是2 | C. | 中位数是2 | D. | 方差是2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?
将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
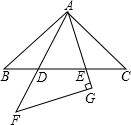
 如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s).
如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
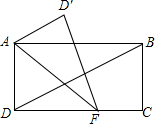 如图把一张长方形线条ABCD 沿AF折叠,使D落在D′处使∠ABD=20°,AD′∥DB则∠DAF的度数为( )
如图把一张长方形线条ABCD 沿AF折叠,使D落在D′处使∠ABD=20°,AD′∥DB则∠DAF的度数为( )| A. | 60° | B. | 55° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
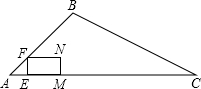
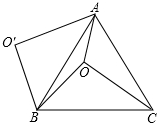 如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$
如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④${S_{四边形AOBO'}}=24+12\sqrt{3}$| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com