
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
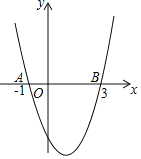
A. ①③ B. ②③ C. ②④ D. ③④
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】折纸中的数学:打开本指书刊幅面的规格大小.如图①,将一张矩形印刷用纸对折后可以得到2开纸,再对折得到4开纸,以此类推可以得到8开纸、16开纸……
若这张矩形印刷用纸的短边长为a.
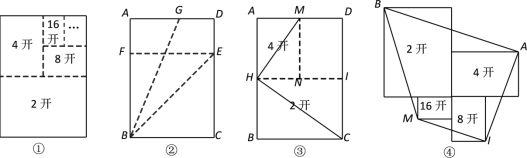
(1)如图②,若将这张矩形印刷用纸ABCD(AB>BC)进行折叠,使得BC与AB重合,点C落在点F处,得到折痕BE;展开后,再次折叠该纸,使点A落在E处,此时折痕恰好经过点B,得到折痕BG,求![]() 的值.
的值.
(2)如图③,②中的矩形纸片ABCD折成2开纸BCIH和4开纸AMNH,它们的对角线分别是HC、HM.说明HC⊥HM.
(3)将图①中的2开纸、4开纸、8开纸和16开纸按如图④所示的方式摆放,依次连接点A、B、M、I,则四边形ABMI的面积是 .(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
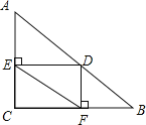
【题目】如图,在△ABC中,AB=10,BC=8,AC=6.点D在AB边上(不包括端点),DE⊥AC,DF⊥BC,垂足分别为点E和点F,连结EF.
(1)判断四边形DECF的形状,并证明;
(2)线段EF是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填幻方:将1、2、3、4、5、6、7、8、9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字2、4固定在图中所示的位置时,按规则填写空格,所有可能出现的结果有( )
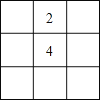
A.4种B.6种C.8种D.9种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣![]() ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
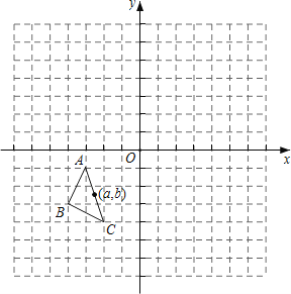
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
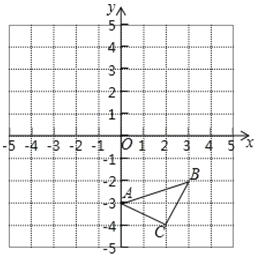
【题目】如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(0,-3),B(3,-2),C(2,-4).
(1)在图中作出△ABC关于x轴对称的△A1B1C1.
(2)点C1的坐标为: .
(3)△ABC的周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com