
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.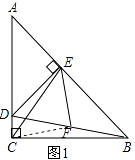
(1)若AD=3 ![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE= ![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
【答案】
(1)
解:∵∠AED=90°,AE=DE,AD=3 ![]() ,
,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF= ![]() BD=2.5
BD=2.5
(2)
解:如图1,连接CF,线段CE与FE之间的数量关系是CE= ![]() FE;
FE;
解法1:∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE= ![]() EF.
EF.
解法2:∵∠BED=∠AED=∠ACB=90°,
∵点F是BD的中点,
∴CF=EF=FB=FD,
∵∠DFE=∠ABD+∠BEF,∠ABD=∠BEF,
∴∠DFE=2∠ABD,
同理∠CFD=2∠CBD,
∴∠DFE+∠CFD=2(∠ABD+∠CBD)=90°,
即∠CFE=90°,
∴CE= ![]() EF.
EF.
(3)
解:解法1:如图2﹣1,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
 ,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE= ![]() FE;
FE;
解法2:如图2﹣2,连结CF、AF,
∵∠BAD=∠BAC+∠DAE=45°+45°=90°,
又∵点F是BD的中点,
∴FA=FB=FD,
在△ACF和△BCF中,
 ,
,
∴△ACF≌△BCF,
∴∠ACF=∠BCF= ![]() ∠ACB=45°,
∠ACB=45°,
∵FA=FB,CA=CB,
∴CF所在的直线垂直平分线段AB,
同理,EF所在的直线垂直平分线段AD,
又∵DA⊥BA,
∴EF⊥CF,
∴△CEF为等腰直角三角形,
∴CE= ![]() EF.
EF.

【解析】(1)由AE=DE,∠AED=90°,AD=3 ![]() ,可求得AE=DE=3,在Rt△BDE中,由DE=3,BE=4,可知BD=5,又F是线段BD的中点,所以EF=
,可求得AE=DE=3,在Rt△BDE中,由DE=3,BE=4,可知BD=5,又F是线段BD的中点,所以EF= ![]() BD=2.5;(2)连接CF,直角△DEB中,EF是斜边BD上的中线,因此EF=DF=BF,∠FEB=∠FBE,同理可得出CF=DF=BF,∠FCB=∠FBC,因此CF=EF,由于∠DFE=∠FEB+∠FBE=2∠FBE,同理∠DFC=2∠FBC,因此∠EFC=∠EFD+∠DFC=2(∠EBF+∠CBF)=90°,因此△EFC是等腰直角三角形,CF=
BD=2.5;(2)连接CF,直角△DEB中,EF是斜边BD上的中线,因此EF=DF=BF,∠FEB=∠FBE,同理可得出CF=DF=BF,∠FCB=∠FBC,因此CF=EF,由于∠DFE=∠FEB+∠FBE=2∠FBE,同理∠DFC=2∠FBC,因此∠EFC=∠EFD+∠DFC=2(∠EBF+∠CBF)=90°,因此△EFC是等腰直角三角形,CF= ![]() EF;(3)思路同(1).连接CF,延长EF交CB于点G,先证△EFC是等腰三角形,要证明EF=FG,需要证明△DEF和△FGB全等.由全等三角形可得出ED=BG=AD,又由AC=BC,因此CE=CG,∠CEF=45°,在等腰△CFE中,∠CEF=45°,那么这个三角形就是个等腰直角三角形,因此得出结论.
EF;(3)思路同(1).连接CF,延长EF交CB于点G,先证△EFC是等腰三角形,要证明EF=FG,需要证明△DEF和△FGB全等.由全等三角形可得出ED=BG=AD,又由AC=BC,因此CE=CG,∠CEF=45°,在等腰△CFE中,∠CEF=45°,那么这个三角形就是个等腰直角三角形,因此得出结论.
【考点精析】认真审题,首先需要了解图形的旋转(每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图是2015年12月月历.
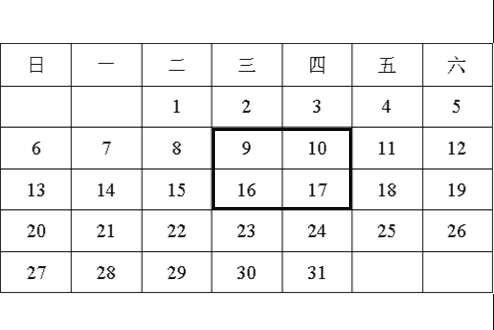
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
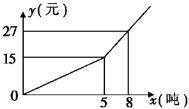
【题目】某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,
(1)分别写出x≤5和x>5的函数解析式;
(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;
(3)若某户居民六月交水费31元,则用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
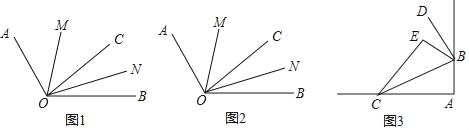
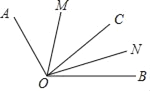
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数 | 60° | 90° | 120° |
∠MON的度数 |
|
|
|
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式,你发现了什么规律?
12=![]() ;12+22=
;12+22=![]() ;12+22+32=
;12+22+32=![]() ;12+22+32+42=
;12+22+32+42=![]() ;…
;…
①根据你发现的规律,计算下面算式的值;12+22+32+42+52=____________;
②请用一个含n的算式表示这个规律:12+22+32…+n2=___________;
③根据你发现的规律,计算下面算式的值:512+522+…+992+1002=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com