
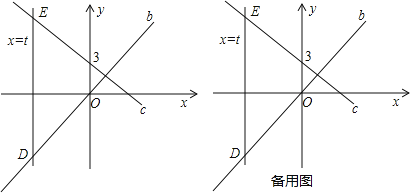
【题目】如图,已知直线c和直线b相较于点![]() ,直线c过点
,直线c过点![]() 平行于y轴的动直线a的解析式为
平行于y轴的动直线a的解析式为![]() ,且动直线a分别交直线b、c于点D、
,且动直线a分别交直线b、c于点D、![]() 在D的上方
在D的上方![]() .
.
![]() 求直线b和直线c的解析式;
求直线b和直线c的解析式;
![]() 若P是y轴上一个动点,且满足
若P是y轴上一个动点,且满足![]() 是等腰直角三角形,求点P的坐标.
是等腰直角三角形,求点P的坐标.
【答案】(1)![]() ,
,![]() (2)当
(2)当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]() 或
或![]() ;当
;当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]() ;当
;当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]()
【解析】
![]() 设直线b的解析式为
设直线b的解析式为![]() ,设直线c的解析式为:
,设直线c的解析式为:![]() ,把点的坐标代入即可得到结论;
,把点的坐标代入即可得到结论;
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,得到E点坐标为
,得到E点坐标为![]() ,D点坐标为
,D点坐标为![]() 分三种情况:
分三种情况:![]() 若
若![]() ,
,![]() 时,
时,![]() 若
若![]() ,
,![]() 时,即DE为斜边,
时,即DE为斜边,![]() 若
若![]() ,
,![]() 时,即DE为斜边,由已知得
时,即DE为斜边,由已知得![]() ,
,![]() ,列方程即可得到结论.
,列方程即可得到结论.
![]() 设直线b的解析式为:
设直线b的解析式为:![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,
![]() 直线b的解析式为:
直线b的解析式为:![]() ;
;
设直线c的解析式为:![]() ,
,
把点![]() ,点
,点![]() 代入得,
代入得,![]() ,
,
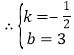 ,
,
![]() 直线c的解析式为:
直线c的解析式为:![]() ;
;
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() ,
,
![]() 点坐标为
点坐标为![]() ,D点坐标为
,D点坐标为![]() .
.
![]() 在D的上方,
在D的上方,
![]() ,且
,且![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() 或
或![]() 或
或![]() .
.
![]() 时,
时,![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,
![]() 若
若![]() ,
,![]() 时,
时,![]() ,
,
![]() 点坐标为
点坐标为![]() ;
;
![]() 若
若![]() ,
,![]() 时,即DE为斜边,
时,即DE为斜边,![]() ,
,
![]() ,DE的中点坐标为
,DE的中点坐标为![]() ,
,
![]() 点坐标为
点坐标为![]()
若![]() ,
,![]() 和
和![]() 时,由已知得
时,由已知得![]() ,
,![]() ,
,![]()
![]() 不符合题意,舍去
不符合题意,舍去![]() ,
,
此时直线![]() 不存在.
不存在.
![]() 若
若![]() ,
,![]() 时,即DE为斜边,由已知得
时,即DE为斜边,由已知得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为![]()
综上所述:当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]() 或
或![]() ;
;
当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]() ;
;
当![]() 时,
时,![]() 为等腰直角三角形,此时P点坐标为
为等腰直角三角形,此时P点坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=﹣![]() x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.
(1)①填空:⊙A的半径为 ,b= .(不需写解答过程)
②判断直线BC与⊙A的位置关系,并说明理由.
(2)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
(3)若点P在⊙A上,点Q是y轴上一点且在点C下方,当△PQM为等腰直角三角形时,直接写出点Q的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一条线段将一个三角形分成2个小等腰三角形,我们把这条线段叫做这个三角形的“好线”:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的“好好线”.
理解:
(1)如图1,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() ,求
,求![]() 的大小;
的大小;
(2)在图1中过点![]() 作一条线段
作一条线段![]() ,使
,使![]() ,
,![]() 是
是![]() 的“好好线”;
的“好好线”;
在图2中画出顶角为![]() 的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);
的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);
应用:
(3)在![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的“好好线”,点
的“好好线”,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() ,请求出
,请求出![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图1,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部C的俯角.

(1)如果上述仰角与俯角分别为30°与60°,且该楼的高度为30米,求该时刻无人机的竖直高度CD;
(2)如图2,如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的面积为1.分别倍长(延长一倍)
的面积为1.分别倍长(延长一倍)![]() ,BC,CA得到
,BC,CA得到![]() .再分别倍长A1B1,B1C1,C1A1得到
.再分别倍长A1B1,B1C1,C1A1得到![]() .…… 按此规律,倍长2018次后得到的
.…… 按此规律,倍长2018次后得到的![]() 的面积为( )
的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知学习,若一条线段把一个平面图形分成面积相等的两部分,我们把这条段线做该平面图形的二分线解决问题:
(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是_______
②如图1,已知△ABC中,AD是BC边上的中线,点E,F分别在AB,DC上,连接EF,与AD交于点G,若![]() 则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.
则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.

(2)如图2,四边形ABCD中,CD平行于AB,点G是AD的中点,射线CG交射线BA于点E,取EB的中点F,连接CF.求证:CF是四边形ABCD的二分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:



(1)求证:EP2+GQ2=PQ2;
(2)若将Rt△EFG绕着点A逆时针旋转α(0°<α≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由;
(3)若将Rt△EFG绕着点A逆时针旋转α(90°<α<180°),两直角边所在的直线分别交BA、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com