【题目】如图，一次函数y=kx+b的图象分别与反比例函数y=
的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．
（1）求函数y=kx+b和y=
的表达式；
（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标．
【答案】（1）y=2x﹣5,y=
;（2）（2.5，0）．
【解析】（1）利用待定系数法即可解答；
（2）设点M的坐标为（x，2x﹣5），根据MB=MC，得到
，即可解答．
（1）把点A（4,3）代入函数y=
得：a=3×4=12，∴y=
．OA=
=5，
∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5），
把B（0，﹣5），A（4，3）代入y=kx+b得：
解得：
∴y=2x﹣5．
（2）∵点M在一次函数y=2x﹣5上，∴设点M的坐标为（x，2x﹣5），
∵MB=MC，∴
解得：x=2.5，∴点M的坐标为（2.5，0）．
“点睛”本题考查了一次函数与反比例函数的交点，解决本题的关键是利用待定系数法求解析式.
科目：初中数学 来源： 题型：
【题目】某中学为了了解2018年度下学期七年级数学学科期末考试各分数段成绩的分布情况，从全校七年级1200名学生中随机抽取了200名学生的期末数学成绩进行调查，在这次调查中，样本是( )
A. 1200名学生 B. 200名学生
C. 1200名学生的期末数学成绩 D. 200名学生的期末数学成绩
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是40cm．求：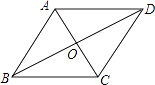 
（1）两条对角线AC、BD的长度；
（2）菱形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若抛物线L：y=ax2+bx+c（a，b，c是常数，abc≠0）与直线l都经过y轴上的一点P，且抛物线L的顶点Q在直线l上，则称此直线l与该抛物线L具有“一带一路”关系．此时，直线l叫做抛物线L的“带线”，抛物线L叫做直线l的“路线”．
（1）若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系，求m，n的值；
（2）若某“路线”L的顶点在反比例函数y=
的图象上，它的“带线”l的解析式为y=2x﹣4，求此“路线”L的解析式；
（3）当常数k满足
≤k≤2时，求抛物线L：y=ax2+（3k2﹣2k+1）x+k的“带线”l与x轴，y轴所围成的三角形面积的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用配方法解一元二次方程x2﹣4x﹣5=0的过程中，配方正确的是( )
A. （x+2）2=1B. （x﹣2）2=1C. （x+2）2=9D. （x﹣2）2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
