
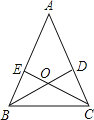
【题目】如图,△ABC中,AB=AC,两条角平分线BD、CE相交于点O.
(1)证明:△ABD≌△ACE;(2)证明:OB=OC.
【答案】见解析
【解析】试题分析:(1)、根据等腰三角形的性质和角平分线的性质得出∠ABD=∠ACE,然后结合∠A=∠A,AB=AC,根据ASA来判定两个三角形全等;(2)、根据等腰三角形和角平分线的性质得出∠DBC=∠ECB,从而得到△OBC为等腰三角形,从而得出答案.
试题解析:(1)证明:∵AB=AC,
∴∠ABC=∠ACB
∵两条角平分线BD、CE相交于点O
∴∠ABD=∠ACE,
在△ABD和△ACE中,
∠ABD=∠ACE,AB=AC,∠A=∠A,
△ABD≌△ACE.
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵两条角平分线BD、CE相交于点O
∴∠DBC=∠ECB
∴OB=OC


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作题:公元初,中美洲玛雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“”划“”、卵形“![]() ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.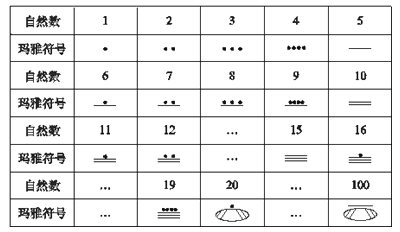
(1)玛雅符号 ![]() 表示的自然数是 ;
表示的自然数是 ;
(2)请你在右边的方框中画出表示自然数280的玛雅符号: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
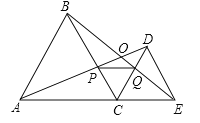
①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了丰富社会实践活动,引导学生科学探究,学校组织七年级同学走进中国科技馆,亲近科学,感受科技魅力.来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④号小球向下运动,运动速度均为3米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为2米/秒,当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚![]() 秒到达相应位置,问②号小球运动了多少米?
秒到达相应位置,问②号小球运动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() (其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m).点A关于直线l的对称点为B,作BC⊥x轴于点C,连接PC、PB,与抛物线、x轴分别相交于点D、E,连接DE.将△PBC沿直线PB翻折,得到△PBC′.
(1)该抛物线的解析式为 ; (用含m的式子表示);
(2)探究线段DE、BC的关系,并证明你的结论;
(3)直接写出C′点的坐标(用含m的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com