
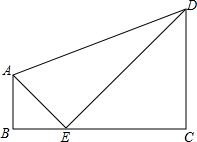
 如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,
如图,已知直角梯形ABCD中,∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,分析 根据已知条件得到△ABE与△CDE是等腰直角三角形,由等腰直角三角形的性质得到∠AEB=∠DEC=45°,AE=$\sqrt{2}$a,DE=$\sqrt{2}$b,求得∠AED=90°,然后根据三角形和梯形的面积公式即可得到(1),(2),(3)的结果.
解答 解:∵∠ABC=∠DCB=90°,点E在高上,且BE=AB=a,CE=CD=b,
∴△ABE与△CDE是等腰直角三角形,
∴∠AEB=∠DEC=45°,AE=$\sqrt{2}$a,DE=$\sqrt{2}$b,
∴∠AED=90°,
(1)S△ECD=$\frac{1}{2}$CE•CD=$\frac{1}{2}$b2;
(2)S梯形ABCD=$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a+b)2;
(3)S△ADE=$\frac{1}{2}$AE•DE=$\frac{1}{2}$×$\sqrt{2}$a×$\sqrt{2}$b=ab.
点评 本题考查了列代数式,等腰直角三角形的判定和性质,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 支撑物高度h/cm | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 小车下滑时间t/s | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 |
| A. | 支撑物的高度为40cm,小车下滑时间为2.13s | |
| B. | 支撑物高度h越大,小车下滑时间t越小 | |
| C. | 若小车下滑时间为2s,则支撑物高度在40cm至50cm之间 | |
| D. | 若支撑物的高度为80cm,则小车下滑时间可以使小于1.59s的任意值 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
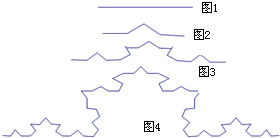 若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$.
若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (2)(4) | C. | (1)(4) | D. | (1)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
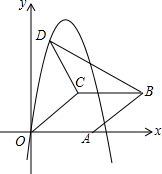 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com