
科目:初中数学 来源: 题型:
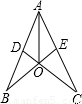
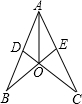 小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.
小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动中,爱动脑筋的小华同学设计了一个几何模型:将一个面积为1的正方形按照图示进行分割.研究发现,图中蕴含着一个美妙的数量关系.
在一次数学活动中,爱动脑筋的小华同学设计了一个几何模型:将一个面积为1的正方形按照图示进行分割.研究发现,图中蕴含着一个美妙的数量关系.| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 34 |
| 1 |
| 35 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
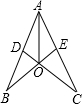 小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.
小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com