
 如图,已知:等边三角形ABC中内有一点P,PA=4,PC=3,PB=5,求∠APC的度数.
如图,已知:等边三角形ABC中内有一点P,PA=4,PC=3,PB=5,求∠APC的度数. 分析 根据题意,通过顺时针旋转,可以得到△ADB与△APC的关系,通过转化可以求得∠ADB的度数,从而可以求得∠APC的度数.
解答 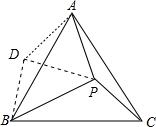 解:如图,∵△ABC为等边三角形,
解:如图,∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°;
将△APC按顺时针旋转60°,得到△ADB,
∴AD=AP=PD,DB=CP,∠ADB=∠APC,
∴△ADP是等边三角形,
∴∠ADP=60°,
∵AP=4,PC=3,
∴BD=CP=3,PD=AP=4,BP=5,
∵32+42=52,
∴△BDP是直角三角形,∠BDP=90°,
∴∠ADB=∠ADP+∠BDP=60°+90°=150°,
∴∠APC=150°.
点评 本题考查勾股定理的逆定理、等边三角形的性质、旋转的性质,解题的关键是明确题意,利用数形结合的思想解答.


科目:初中数学 来源: 题型:解答题
 如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,
如图,一块大的三角板ABC,D是AB上一点,现要求过点D割出一块小的三角板ADE,使∠ADE=∠ABC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 旋转时间x/min | 0 | 3 | 6 | 8 | 12 | … |
| 高度y/m | 5 | 70 | 5 | 54 | 5 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数.
求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com