
【题目】如图,矩形纸片ABCD,BC=10,AB=8,E是边CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为____.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】佛山一环高速化改造后正式收费,车辆经过平胜大桥收费站时,设置了 4 个 ETC 智能收费(即不 需要人工收费)通道,分别为 A、B、C、D 通道,车辆可随机选择其中的一个直接读卡通过.
(1)一辆车经过此收费站时,选择 A 通道通过的概率是___________;
(2)现有甲、乙两辆小车从同一方向通过此收费站,请你用树状图或列表格求出两辆车选择不同通道通过的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.
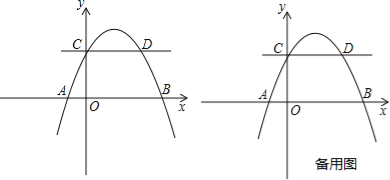
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5 小时内其血液中酒精含量 y(毫克/百毫升) 与时间 x(时)的关系可近似地用二次函数 y=﹣200x2+400x 刻画;1.5 小时后(包括 1.5 小时)y 与 x 可近似地用反比例函数![]()
![]() 刻画(如图所示)
刻画(如图所示)
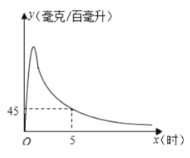
(1)根据上述数学模型计算:喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于 20 毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上 20:00 在家喝完半斤低度白酒,第二天早上 7:00 能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低1元,每天可多售出200斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
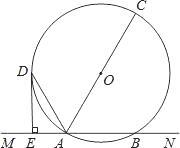
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com