
如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.

|
| A. | 156 | B. | 157 | C. | 158 | D. | 159 |
考点:
规律型:图形的变化类.
分析:
根据第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,得出规律第n个图案需n(n+3)+3根火柴,再把11代入即可求出答案.
解答:
解:根据题意可知:
第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…,
第n个图案需n(n+3)+3根火柴,
则第11个图案需:11×(11+3)+3=157(根);
故选B.
点评:
此题主要考查了图形的变化类,关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,再利用规律解决问题,难度一般偏大,属于难题.


科目:初中数学 来源: 题型:

| 分割次数(n) | 1 | 2 | 3 | … | ||
| 一个最小等边三角形的面积(S) |
|
… |
查看答案和解析>>
科目:初中数学 来源: 题型:
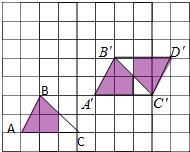 如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题:
如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 分割次数(n) | 1 | 2 | 3 | … |
| 一个最小等边三角形的面积(S) |  a a | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
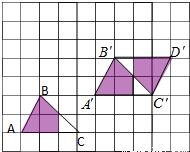
 如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题:
如图,在方格纸(每个小方格都是边长为1个单位长度的正方形)上,并且图形的顶点均在格点上,请结合所给的方格纸解答下列问题:查看答案和解析>>
科目:初中数学 来源:2010年海南省中考数学模拟试卷(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com