
【题目】已知在△ABC中,AC=BC,分别过A,B两点作互相平行的直线AM,BN,过点C的直线分别交直线AM,BN于点D,E.

(1)如图1,若AM⊥AB,求证:CD=CE;
(2)如图2,∠ABC=∠DEB=60°,判断线段AD,DC与BE之间的关系,并说明理由.
【答案】(1)见解析;(2)AD+DC=BE,理由见解析
【解析】
(1)延长AC交BN于点F,证明△ADC≌△FEC(ASA),即可得出结论;
(2)在EB上截取EH=EC,连接CH,证明△DAC≌△HCB(AAS),得出AD=CH,DC=BH,即可得出结论.
(1)证明:如图1,延长AC交BN于点F,
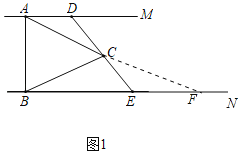
∵AC=BC,
∴∠CAB=∠CBA,
又∵AB⊥AM,
∴∠BAM=90°,
又∵AM∥BN,
∴∠BAM+∠ABN=180°,
∴∠ABN=90°,
∴∠BAF+∠AFB=90°,∠ABC+∠CBF=90°,
∴∠CBF=∠AFB,
∴BC=CF,
∴AC=FC,
又∵AM∥BN,∴∠DAF=∠AFB,
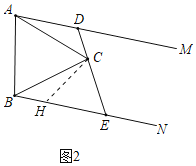
在△ADC和△FEC中,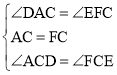 ,
,
∴△ADC≌△FEC(ASA),
∴DC=EC;
(2)解:AD+DC=BE;理由如下:
如图2,在EB上截取EH=EC,连接CH,
∵AC=BC,∠ABC=60°,
∴△ABC为等边三角形,
∵∠DEB=60°,
∴△CHE是等边三角形,
∴∠CHE=60°,∠HCE=60°,
∴∠BHC=120°,
∵AM∥BN,
∴∠ADC+∠BEC=180°,
∴∠ADC=120°,
∴∠DAC+∠DCA=60°,
又∵∠DCA+∠ACB+∠BCH+∠HCE=180°,
∴∠DCA+∠BCH=60°,
∴∠DAC=∠BCH,
在△DAC与△HCB中,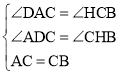 ,
,
∴△DAC≌△HCB(AAS),
∴AD=CH,DC=BH,
又∵CH=CE=HE,
∴BE=BH+HE=DC+AD,
即AD+DC=BE.


科目:初中数学 来源: 题型:
【题目】如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.


(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .设
.设![]() ,点
,点![]() 是直线
是直线![]() 上的动点,当
上的动点,当![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 是否可能重合?若可能,请说明理由并求此时
是否可能重合?若可能,请说明理由并求此时![]() 的值(用含
的值(用含![]() 的式子表示);若不可能,请说明理由.
的式子表示);若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展乡村旅游,某村准备在河道上修一座与河道垂直的桥,如图(1)所示,直线l,m代表河流的两岸河道,且l∥m,点A是某村自助农场的所在地,点B是某村游乐场所在地.

问题1:造桥选址桥准备选在到A,B两地的距离之和刚好为最小的点C处,即在直线l上找一点C,使AC+BC的值为最小.请利用你所学的知识在图(1)中作出点C的位置,并简单说明你所设计方案的原理;
问题2:测量河宽:在测量河道的宽度时施工队在河道南侧的开阔地用以下方法(如图2所示):①作CD⊥l,与河对岸的直线m相交于D;②在直线m上取E,F两点,使得DE=EF=10米;③过点F作m的垂线FG,使得点G与C,E两点在同一直线上;④测量FG的长度为20米.请你确定河道的宽度,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条船上午![]() 点在
点在![]() 处望见西南方向有一座灯塔
处望见西南方向有一座灯塔![]() (如图),此时测得船和灯塔相距
(如图),此时测得船和灯塔相距![]() 海里,船以每小时
海里,船以每小时![]() 海里的速度向南偏西
海里的速度向南偏西![]() 的方向航行到
的方向航行到![]() 处,这时望见灯塔在船的正北方向.(参考数据:
处,这时望见灯塔在船的正北方向.(参考数据:![]() ,
,![]() ).
).

![]() 求几点钟船到达
求几点钟船到达![]() 处;
处;
![]() 求船到达
求船到达![]() 处时与灯塔
处时与灯塔![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a使关于x的不等式组 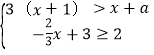 有两个整数解,且使关于x的方程
有两个整数解,且使关于x的方程![]() 有负数解,则符合题意的整数a的个数有 ( )
有负数解,则符合题意的整数a的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 是两个边长都为
是两个边长都为![]() 的等边三角形,且点
的等边三角形,且点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上,连接
在同一直线上,连接![]() ,
,![]() .
.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() 沿着
沿着![]() 的方向匀速运动,
的方向匀速运动,![]() 不动,当
不动,当![]() 运动到点
运动到点![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是什么特殊的四边形?说明理由.
是什么特殊的四边形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com