
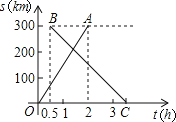
����Ŀ��������̨��������֮�俪ͨ�˶���������г�����֪ÿ��1h��һ���ٶ���ͬ�Ķ������г�����������̨�ݣ���ͼ��ʾ��OA�ǵ�һ�ж������г��뿪������·��s(��λ��km)������ʱ��t(��λ��h)�ĺ���ͼ��BC��һ�д�̨�ݿ�����������ͨ�쳵��������·��s(��λ��km)������ʱ��t(��λ��h)�ĺ���ͼ�������ͼ����Ϣ������������⣺
(1)��B������0.5����������ͨ�쳵�ķ���ʱ��ȵ�һ�ж������г��ķ���ʱ������ ��h����B��������300���������� ����
(2)����ͨ�г����ٶ�Ϊ100km/h��
����BC�Ľ���ʽ��
����ڶ��ж������г�������ʱ������ͨ�г�������
���𰸡���1����0.5���������300km����1����s����100t+350���ڵڶ��ж������г�������1Сʱ����ͨ�г�������
��������
��1����ͼ��֪����ͨ�쳵�ķ���ʱ��ȵ�һ�ж������г��ķ���ʱ����0.5Сʱ���������300km��
��2�����������֪��B��0.5��300����C��3.5��0�����ô���ϵ����������ã�����ͼ�ɵ�MN�Ľ���ʽ������150t-150=-100t+350�������tֵ�����ɽ��
��1����0.5���������300km��
��2������ֱ��BC�Ľ���ʽΪs��kt+b��
��B��0.5��300����C��3.5��0����
��![]() ��
��
���![]() ��
��
��s����100t+350��
����ڶ��ж������г�MN�Ľ���ʽΪs��k1t+b1��
��M��1��0����N��3��300����
��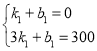 ��
��
���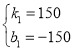 ��
��
��s��150t��150��
�ɢٿ�ֱ֪��BC�Ľ���ʽΪs����100t+350��
��150t��150����100t+350��
���t��2��
��2��1��1��
�𣺵ڶ��ж������г�������1Сʱ����ͨ�г�������




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
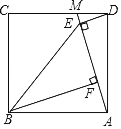
����Ŀ����������ȫ�غϵľ���ֽƬ��С��ͬѧ������һ���Ƶ�A˳ʱ����ת90���õ�����AMEF����ͼ1��������BD��MF������ʱ�����BD=8cm����ADB=30�ȣ���ش��������⣺��1����̽���߶�BD���߶�MF�Ĺ�ϵ������Ҫ˵�����ɣ�
��2��С��ͬѧ�ü�������BCD���MEF��ȥ����С��ͬѧ����̽�������ǽ���ABD�Ƶ�A˳ʱ����ת�á�AB1D1��AD1��FM�ڵ�K����ͼ2��������ת��Ϊ�£�0�㣼�£�90�㣩������AFKΪ����������ʱ����ֱ��д����ת�ǦµĶ�����
��3��������AFM��AB����ƽ�Ƶõ���A2F2M2����ͼ3����F2M2��AD���ڵ�P��A2M2��BD���ڵ�N����NP��ABʱ����ƽ�Ƶľ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
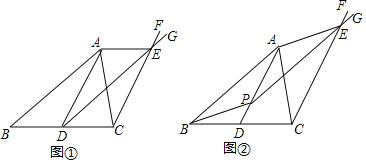
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�����C��ֱ��CF��AD��
�����⣩��ͼ��������D��ֱ��DG��AB��ֱ��CF�ڵ�E������AE����֤��AB��DE��
��̽������ͼ�������߶�AD����ȡһ��P������P��ֱ��PG��AB��ֱ��CF�ڵ�E������AE��BP��̽���ı���ABPE�����������ı��β�����֤����
��Ӧ�ã���̽���������£���PE��AC�ڵ�M������P��AD���е㣬�ҡ�APM�����Ϊ1��ֱ��д���ı���ABPE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��������ABCD��CD��һ�㣬����AM����DE��AM�ڵ�E��BF��AM�ڵ�F������BE����AF��1���ı���ABED�����Ϊ6�����EBF������ֵ�ǣ�������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
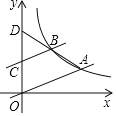
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��˫����
��˫����![]() ���ڵ�A������
���ڵ�A������![]() ��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�
��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�![]() ����k��ֵΪ______��
����k��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
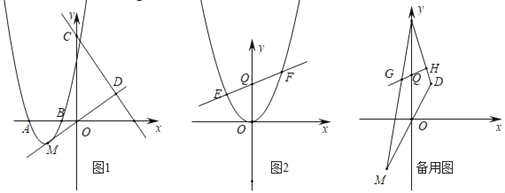
����Ŀ����ͼ1��������y��ax2+bx+3������A(��3��0)��B(��1��0)���㣬�����ߵĶ���ΪM��ֱ��y����4x+9��y�ύ�ڵ�C����ֱ��OM���ڵ�D��
(1)�������ߵĽ���ʽ��
(2)��Q(0��3)����ƽ����x���ֱ��l
����ͼ2����������ƽ�ƣ���������ԭ��ʱ��ֱ��l���������ڵ�E��F����y���ϴ���һ��P��ʹ��PEF��������y���ϣ����P�����ꣻ
��ֱ��l����CMD�ı�CM��CD�ڵ�G��H(G�㲻��M���غϡ�H�㲻��D���غ�)��S�ı���MDHG��S��CGH�ֱ��ʾ�ı���MDHG�͡�CGH���������̽��![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=4��BC=6��E��BC�ߵ��е㣬��P���߶�AD�ϣ���P��PF��AE��F����PA=x��
��1����֤����PFA�ס�ABE��
��2������P���߶�AD���˶�ʱ����PA=x���Ƿ����ʵ��x��ʹ���Ե�P��F��EΪ�����������Ҳ����ABE���ƣ������ڣ������x��ֵ���������ڣ���˵�����ɣ�
��3��̽��������DΪԲ�ģ�DPΪ�뾶�ġ�D���߶�AEֻ��һ��������ʱ����ֱ��д��x������������� ����

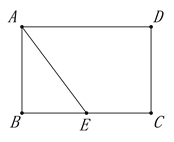
����ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
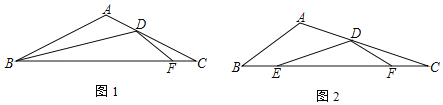
����Ŀ���ڡ�ABC�У���E��F�ڱ�BC�ϣ���D�ڱ�AC�ϣ�����ED��DF��![]() ��m����A����EDF��120��
��m����A����EDF��120��
��1����ͼ1����E��B�غϣ�m��1ʱ
����BDƽ�֡�ABC����֤��CD2��CFCB��
����![]() ����
����![]() ���� ����
���� ����
��2����ͼ2����E��B���غϣ���BE��CF��![]() ��m��
��m��![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com