
 已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.
已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:选择题
如图,在直角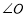 的内部有一滑动杆
的内部有一滑动杆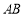 .当端点
.当端点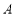 沿直线
沿直线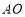 向下滑动时,端点
向下滑动时,端点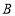 会随之自动地沿直线
会随之自动地沿直线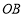 向左滑动.如果滑动杆从图中
向左滑动.如果滑动杆从图中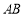 处滑动到
处滑动到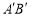 处,那么滑动杆的中点
处,那么滑动杆的中点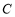 所经过的路径是( )
所经过的路径是( )
A.直线的一部分 B.圆的一部分
C.双曲线的一部分 D.抛物线的一部分
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
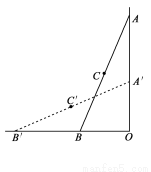
 如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,CD=CB,求证:
如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,CD=CB,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
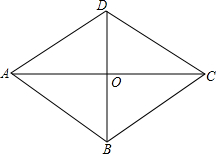 如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:
如图,菱形ABCD中,AC,BD交于点O,AC=8cm BD=6cm,动点M从A点出发沿AC方向以2cm/s匀速直线运动到C点,动点N从B点出发沿BD方向以1cm/s匀速直线运动到D点,若M,N同时出发,设运动时间为t秒:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
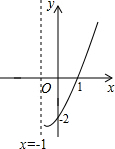 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2-4ac>0;③a-b+c=0;④2a-b=0.正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com