
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
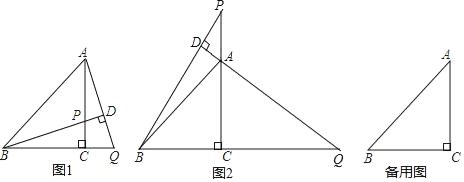
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
【答案】(1)证明见解析;(2)(2)成立,理由见解析;(3)当∠DBA=22.5°时,存在AQ=2BD,理由见解析.
【解析】试题分析:(1)首先根据内角和定理得出∠DAP=∠CBP,进而得出
△ACQ≌△BCP即可得出答案;
(2)延长BA交PQ于H,由于![]() 得到
得到![]() 推出△AQC≌△BPC(ASA),即可得出结论;
推出△AQC≌△BPC(ASA),即可得出结论;
(3)当![]() 时,存在
时,存在![]() 根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
根据等腰三角形的性质得到BP=2BD,通过△PBC≌△ACQ,根据全等三角形的性质即可得到结论.
试题解析:
(1)证明:∵∠ACB=∠ADB=90°,∠APD=∠BPC,
∴∠DAP=∠CBP,
在△ACQ和△BCP中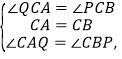
∴△ACQ≌△BCP(ASA),
∴BP=AQ
(2)成立,
理由:延长BA交PQ于H,
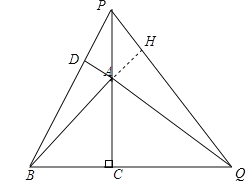
![]() ∠AQC=∠BQD,
∠AQC=∠BQD,
∴∠CAQ=∠DBQ,
在△AQC和△BPC中,
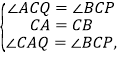
∴△AQC≌△BPC(ASA),
∴AQ=BP,
故答案为:成立;
(3)22.5°,
当∠DBA=22.5°时,存在AQ=2BD,
理由:∵∠BAC=∠DBA+∠APB=45°,
∴∠PBA=∠APB=22.5°,
∴AP=AB,
∵AD⊥BP,
∴BP=2BD,
在△PBC与△QAC中,
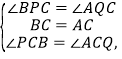
∴△PBC≌△ACQ,
∴AQ=PB,
∴AQ=2BD.
故答案为:22.5°.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
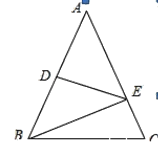
【题目】如图,已知AB=AC,DE垂直平分AB交AC、AB于E、D两点,若AB=12cm,BC=10cm,∠A=50°,求△BCE的周长和∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC⊥AC,BC=8,AC=6,AB=10,则点 C 到线段 AB 的距离是_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923292236627968/1924724835434496/STEM/46ca9c8351da4594816ea507a60c9cdd.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:第一个数是 ![]() ;第二个数是
;第二个数是 ![]() ;第三个数是
;第三个数是 ![]() ;
;
(1)经过探究,我们发现: ![]() ,
, ![]() ,
,
设这列数的第 5 个数为 a ,那么 ![]() ,a=
,a=![]() ,a<
,a<![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数 (即用正整数n表示第 n 数),并且证明你的猜想满足"第n个数与第 (n+1) 个数的和等于 ![]() ";
";
(3)设 ![]() 表示
表示 ![]() ,这 2016个数的和,
,这 2016个数的和,
即 M=![]() .
.
求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.你认为这个规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
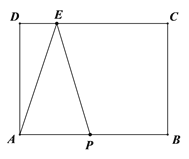
【题目】如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD边上的一点,且DE=2cm,动点P从A点出发,以2cm/s的速度沿A→B→C→E运动,最终到达点E.当△APE的面积等于20cm2时,求点P运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD为AB边上的高,E是AB上一点,且CE=BE.
(1)写出图中所有的等腰三角形:______________________________
(2)写出图中所有的等边三角形:______________________________
(3)若DE=2cm,则AB=______cm,AC=______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com