【题目】一辆客车从甲地开住乙地，一辆出租车从乙地开往甲地，两车同时出发，两车距甲地的距离y（千米）与行驶时间式（小时）之间的函数图象如图所示，则下列说法中错误的是（ ）
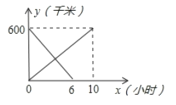
A. 客车比出租车晚4小时到达目的地B. 客车速度为60千米时，出租车速度为100千米/时
C. 两车出发后3.75小时相遇D. 两车相遇时客车距乙地还有225千米
【答案】D
【解析】
观察图形可发现客车出租车行驶路程均为600千米，客车行驶了10小时，出租车行驶了6小时，即可求得客车和出租车行驶时间和速度；
易求得直线AC和直线OD的解析式，即可求得交点横坐标x，即可求得相遇时间，和客车行驶距离，即可解题．
解：（1）∵客车行驶了10小时，出租车行驶了6小时，∴客车比出租车晚4小时到达目的地，故A正确；
（2）∵客车行驶了10小时，出租车行驶了6小时，∴客车速度为60千米/时，出租车速度为100千米/时，故B正确；
（3）∵设出租车行驶时间为x，距离目的地距离为y，
则y＝100x＋600，
设客车行驶时间为x，距离目的地距离为y，
则y＝60x；
当两车相遇时即60x＝100x＋600时，x＝3.75h，故C正确；
∵3.75小时客车行驶了60×3.75＝225千米，
∴距离乙地600225＝375千米，故D错误；
故选：D．
科目：初中数学 来源： 题型：
【题目】矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（ ）
A. 1 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
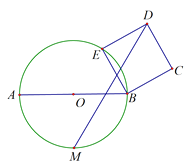
【题目】如图：已知⊙O的半径为6，E是⊙O上一个动点，以BE为边按顺时针方向做正方形BEDC，M是弧AB的中点，当E在圆上移动时，MD的最小值是_______
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】三角形ABC与三角形
在平面直角坐标系中的位置如图所示，三角形是由三角形ABC经过平移得到的．
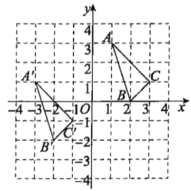
（1）分别写出点
的坐标；
（2）说明三角形是由三角形ABC经过怎样的平移得到的；
（3）若点
是三角形ABC内的一点，则平移后点P在三角形内的对应点为P‘，写出点P’的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB∥CD，解决下列问题：
（1）如图①，写出∠ABE、∠CDE和∠E之间的数量关系： ；
（2）如图②，BP、DP分别平分∠ABE、∠CDE，若∠E＝100°，求∠P的度数；
（3）如图③，若∠ABP＝
∠ABE，∠CDP＝∠CDE，试写出∠P与∠E的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一个三角形纸片的两边长是5和6，第三边的长是方程x2﹣6x+5=0的一个根，若用此三角形纸片剪出一个圆，则剪出的圆的半径最大是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习了数轴后，小亮决定对数轴进行变化应用：
（1）应用一：已知点
在数轴上表示为-2，数轴上任意一点
表示的数为
，则
两点的距离可以表示为 ；应用这个知识，请写出当
时，
有最小值为 ．
（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的
，第二次剪掉剩下的，依此类推，每次都剪掉剩下的，则剪掉4次后剩下线段长度为 ；应用这个原理，请计算：
；
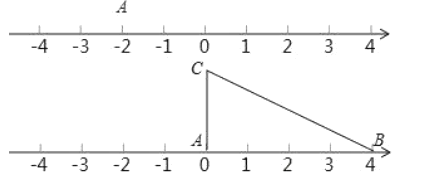
（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为
，
，
的三角形
的顶点与原点重合，边在数轴正半轴上，将数轴正半轴的线沿
的顺序依次缠绕在三角形的边上，负半轴的线沿
的顺序依次缠绕在三角形的边上．
①如果正半轴的线缠绕了3圈，负半轴的线缠绕了5圈，求绕在点
上的所有数之和；
②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点-2的位置对应着拉长后的数-1，并将三角形向正半轴平移一个单位后再开始绕，求绕在点且绝对值不超过60的所有数之和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果零售商店分两批次从批发市场共购进“红富士”苹果100箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款400元．
（1）求第一、二次分别购进“红富士”苹果各多少箱？
（2）商店对这100箱“红富士”苹果先按每箱60元销售了75箱后出现滞销，于是决定其余的每箱靠打折销售完．要使商店销售完全部“红富士”苹果所获得的利润不低于1300元，问其余的每箱至少应打几折销售？（注：按整箱出售，利润＝销售总收人﹣进货总成本）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
