
【题目】如图,已知线段![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,
,![]() 是射线
是射线![]() 上一动点,
上一动点,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,过点
的中点,过点![]() ,
,![]() ,
,![]() 的圆与
的圆与![]() 的另一交点
的另一交点![]() (点
(点![]() 在线段
在线段![]() 上),连结
上),连结![]() ,
,![]() .
.
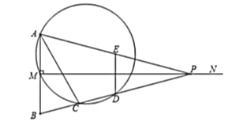
(1)当![]() 时,求
时,求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)在点![]() 的运动过程中,当
的运动过程中,当![]() 时,取四边形
时,取四边形![]() 一边的两端点和线段
一边的两端点和线段![]() 上一点
上一点![]() ,若以这三点为顶点的三角形是直角三角形,且
,若以这三点为顶点的三角形是直角三角形,且![]() 为锐角顶点,求所有满足条件的
为锐角顶点,求所有满足条件的![]() 的值.
的值.
【答案】(1)75°;(2)证明见解析;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据三角形ABP是等腰三角形,可得∠B的度数;
(2)连接MD,根据MD为△PAB的中位线,可得∠MDB=∠APB,再根据∠BAP=∠ACB,∠BAP=∠B,即可得到∠ACB=∠B,进而得出△ABC∽△PBA,得出答案即可;
(3)记MP与圆的另一个交点为R,根据AM2+MR2=AR2=AC2+CR2,即可得到PR=![]() ,MR=
,MR=![]() ,再根据Q为直角三角形锐角顶点,分四种情况进行讨论:当∠ACQ=90°时,当∠QCD=90°时,当∠QDC=90°时,当∠AEQ=90°时,即可求得MQ的值.
,再根据Q为直角三角形锐角顶点,分四种情况进行讨论:当∠ACQ=90°时,当∠QCD=90°时,当∠QDC=90°时,当∠AEQ=90°时,即可求得MQ的值.
解:(1)∵MN⊥AB,AM=BM,
∴PA=PB,
∴∠PAB=∠B,
∵∠APB=30°,
∴∠B=75°,
(2)如图1,连接MD,
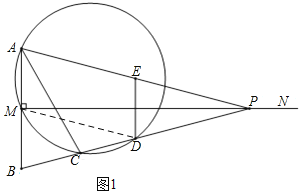
∵MD为△PAB的中位线,
∴MD∥AP,
∴∠MDB=∠APB,
∵∠BAC=∠MDC=∠APB,
又∵∠BAP=180°-∠APB-∠B,∠ACB=180°-∠BAC-∠B,
∴∠BAP=∠ACB,
∵∠BAP=∠B,
∴∠ACB=∠B,
∴AC=AB,由(1)可知PA=PB,
∴△ABC∽△PBA,
∴![]() ,
,
∴AB2=BCPB;
(3)如图2,记MP与圆的另一个交点为R,
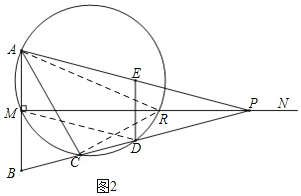
∵MD是Rt△MBP的中线,
∴DM=DP,
∴∠DPM=∠DMP=∠RCD,
∴RC=RP,
∵∠ACR=∠AMR=90°,
∴AM2+MR2=AR2=AC2+CR2,
∴12+MR2=22+PR2,
∴12+(4-PR)2=22+PR2,
∴PR=![]() ,
,
∴MR=![]() ,
,
(一)当∠ACQ=90°时,AQ为圆的直径,
∴Q与R重合,
∴MQ=MR=![]() ;
;
(二)如图3,当∠QCD=90°时,
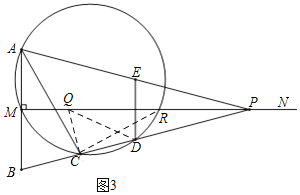
在Rt△QCP中,PQ=2PR=![]() ,
,
∴MQ=![]() ;
;
(三)如图4,当∠QDC=90°时,
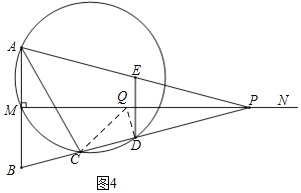
∵BM=1,MP=4,
∴BP=![]() ,
,
∴DP=![]() BP=
BP=![]() ,
,
∵cos∠MPB=![]() ,
,
∴PQ=![]() ,
,
∴MQ=![]() ;
;
(四)如图5,当∠AEQ=90°时,
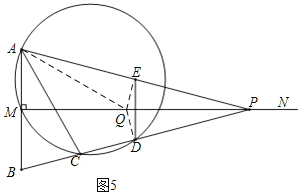
由对称性可得∠AEQ=∠BDQ=90°,
∴MQ=![]() ;
;
综上所述,MQ的值为![]() 或
或![]() 或
或![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
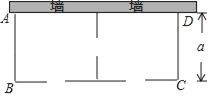
【题目】某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
(1)饲养场的长为多少米(用含a的代数式表示).
(2)若饲养场的面积为288m2,求a的值.
(3)当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块等腰三角形钢板的底边长为![]() ,腰长为
,腰长为![]() .
.
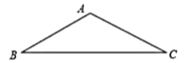
(1)求能从这块钢板上截得的最大圆的半径;
(2)用一个圆完整覆盖这块钢板,这个圆的最小半径是多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
求:(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
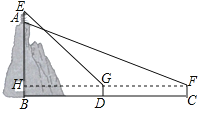
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
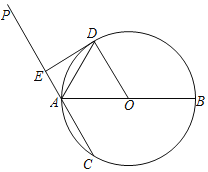
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
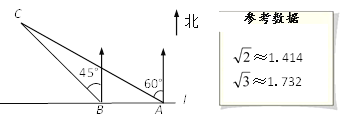
【题目】如图,同学们利用所学知识去测量海平面上一个浮标到海岸线的距离. 在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,小宇同学在A处观测得浮标在北偏西60°的方向,小英同学在距点A处60米远的B点测得浮标在北偏西45°的方向,求浮标C到海岸线l的距离(结果精确到0.01 m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com