练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知关于x的方程x2-3x+k=0，问k取何值时，这个方程：
    （1）有两个不相等的实数根？
    （2）有两个相等的实数根？
    （3）没有实数根？

    分析 （1）由方程有两个不相等的实数根结合根的判别式即可得出关于k的一元一次不等式，解不等式即可得出结论；
    （2）由方程有两个相当的实数根结合根的判别式即可得出关于k的一元一次方程，解方程即可得出结论；
    （3）由方程没有实数根结合根的判别式即可得出关于k的一元一次不等式，解不等式即可得出结论．

    解答 解：（1）∵方程有两个不相等的实数根，
    ∴△=（-3）2-4k＞0，
    解得：k＜$\frac{9}{4}$．
    （2）∵方程有两个相等的实数根，
    ∴△=（-3）2-4k=0，
    解得：k=$\frac{9}{4}$．
    （3）∵方程没有实数根，
    ∴△=（-3）2-4k＜0，
    解得：k＞$\frac{9}{4}$．

    点评 本题考查了根的判别式以及解一元一次不等式，根据方程解的情况结合根的判别式得出关于k的一元一次不等式（或一元一次方程）是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．如图，△ABC的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫做格点三角形，请在图中再画一个格点三角形DEF，使得△DEF≌△ABC，图中最多能画3个格点三角形与△ABC全等（不含△ABC）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算（后两题用简便方法计算）
    （1）20+（-14）-（18）-13     
    （2）（-$\frac{3}{7}$）+$\frac{5}{6}$-（-2$\frac{1}{7}$）+（-$\frac{5}{6}$）
    （3）（-3.2）×$\frac{3}{10}$+（-6.8）×$\frac{3}{10}$
    （4）（-81）÷$\frac{9}{4}$×$\frac{4}{9}$÷（-16）
    （5）（-$\frac{1}{2}$+$\frac{2}{3}$-$\frac{1}{4}$）×（-24）
    （6）-9$\frac{18}{19}$×5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知m与n互为相反数，a，b互为倒数，试求2（m+n）+（-ab）2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）12-（-18）+（-5）-15；
    （2）-81÷$\frac{9}{4}$×（-$\frac{4}{9}$）；
    （3）1÷（$\frac{1}{6}$-$\frac{1}{3}$）×$\frac{1}{2}$； 
     （4）-14-$\frac{1}{6}$×[2-（-3）2]；
    （5）-1.57×（-0.75）+0.57×（-$\frac{3}{4}$）；
    （6）1$\frac{1}{24}$-（$\frac{3}{8}$+$\frac{1}{6}$-$\frac{3}{4}$）×24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

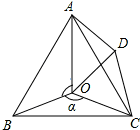    20．如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．
    （1）求证：△ACD≌△BCO；
    （2）当α=150°时，试判断△AOD的形状，并说明理由；
    （3）当△AOD是等腰三角形时，求α的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在△ABC中，AB=AC，AD是BC边上的中线，点E是AC边上一点，且AE=$\frac{1}{3}$AC，连接BE．
    （1）如图1，连接DE，若∠ABC=60°，AC=12，求DE的长．
    （2）如图2，若点F是BE的中点，连接AF并延长交BC于点G，求证：DC=2BG．
    （3）如图3，若∠BAC=90°，过点A作AN⊥BE交BE于点M，连接DM，请直接写出DM与AB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．化简求值：-（3x-2y+z）-[5x-（x-2y+z）-3x]，当x=-2时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知平行四边形ABCD及对角线BD，求作△BCD关于直线BD的对称图形（不要求写作法）．

    查看答案和解析>>

    同步练习册答案