
 .
.
 代入函数的解析式,即可求出t的值.
代入函数的解析式,即可求出t的值.
 ×16=8
×16=8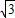 ,
, cm,DC=16cm
cm,DC=16cm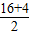 =10(秒),
=10(秒), =12秒,
=12秒,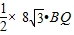 =
=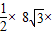 t=4
t=4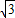 t,
t,
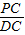 =
= 即
即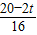 =
=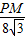 ,
,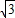 -
- t,
t, BQ•PM
BQ•PM t•(10
t•(10 -
-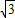 t)
t) t-
t-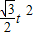 ;
;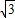 t=
t=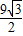 得t=
得t= ;
; t-
t-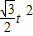 =
=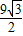 得t=9或t=1(舍去)
得t=9或t=1(舍去) 或t=9时,△PQB的面积为
或t=9时,△PQB的面积为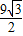 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
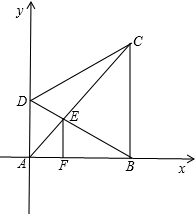 如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.
如图,已知直角梯形ABCD中,AD∥BC∥EF,∠A=90°,BC=DC=4,AC、BD交于E,且EF=ED.查看答案和解析>>
科目:初中数学 来源: 题型:
 21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
21、当我们遇到梯形问题时,我们常用分割的方法,将其转化成我们熟悉的图形来解决:
查看答案和解析>>
科目:初中数学 来源: 题型:
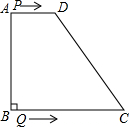
 如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m.
如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD的中点,点F是AB上的点,∠ADF=45°,FE=a,梯形ABCD的面积为m.查看答案和解析>>
科目:初中数学 来源: 题型:
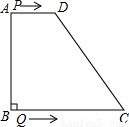
 如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.
如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,∠C=60°,BC=12cm,DC=16cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为y cm2.9
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com