

分析 (1)根据中心关联点的定义,求出R、r、d即可判断;
(2)①由题意可知,点E在直线AM上,当点P在AE上时,点P都是等边△ABC的中心关联点;
②如图1-1中,设平移后的直线交y轴于G,作这条直线的垂线垂足为H.当OH=2时,求出OG即可判断;
(3)存在.理由:如图2中,设Q(m,-1).由题意当OQ=$\frac{3}{2}$时,⊙Q上所有点都是等边△ABC的中心关联点,理由两点间距离公式即可求解.
解答 解:(1)由题意R=2,r=1,点O是△ABC的中心,
∵OD=2$\sqrt{2}$,OE=2,OF=$\frac{\sqrt{5}}{2}$,
∴点E、F是△ABC的中心关联点
故答案为E,F;
(2)①解:如图1中,由题意A(0,2),M($2\sqrt{3}$,0).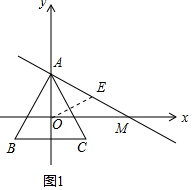
可求得直线AM的解析式为y=-$\frac{\sqrt{3}}{3}$x+2,
经验证E在直线AM上.
因为OE=OA=2,∠MAO=60°,
所以△OAE为等边三角形,
所以AE边上的高长为$\sqrt{3}$.
当点P在AE上时,$\sqrt{3}$≤OP≤2.
所以当点P在AE上时,点P都是等边△ABC的中心关联点.
所以0≤m≤$\sqrt{3}$;
②如图1-1中,设平移后的直线交y轴于G,作这条直线的垂线垂足为H.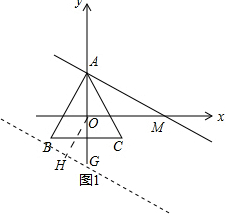
当OH=2时,在Rt△OHG中,∵OH=2,∠HOG=30°,
∴cos30°=$\frac{OH}{OG}$,
∴OG=$\frac{4\sqrt{3}}{3}$,
∴满足条件的b的值为-$\frac{{4\sqrt{3}}}{3}$≤b≤2;
(3)存在.理由:如图2中,设Q(m,-1).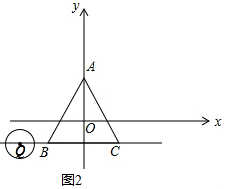
由题意当OQ=$\frac{3}{2}$时,⊙Q上所有点都是等边△ABC的中心关联点,
$\sqrt{{m}^{2}+(-1)^{2}}$=$\frac{3}{2}$,
解得m=$±\frac{\sqrt{5}}{2}$,
∴t=$4-\frac{{\sqrt{5}}}{2}或4+\frac{{\sqrt{5}}}{2}$.
点评 本题考查圆综合题、等边三角形的性质、两点间距离公式、勾股定理、一次函数的应用、锐角三角函数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
 如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )| A. | 10 | B. | 20 | C. | 10+2$\sqrt{2}$ | D. | 10+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3≤m<-2 | B. | -3<m≤-2 | C. | -3≤m≤-2 | D. | -3<m<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.
如图,抛物线表示的是某企业年利润y(万元)与新招员工数x(人)的函数关系,当新招员工200人时,企业的年利润到最大值900万元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 我爱美 | B. | 济南游 | C. | 我爱济南 | D. | 美我济南 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
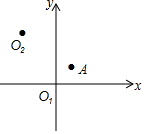 如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2,点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )
如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2,点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )| A. | (3,-2) | B. | (-3,2) | C. | (-2,-3) | D. | (3,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.
如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com