
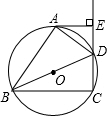
 如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.分析 (1)连接OA,因为点A在⊙O上,所以只要证明OA⊥AE即可;由同圆的半径相等得:OA=OD,则∠ODA=∠OAD,根据角平分线可知:∠OAD=∠EDA,所以EC∥OA,由此得OA⊥AE,则AE是⊙O的切线;
(2)过点O作OF⊥CD,垂足为点F,证明四边形AOFE是矩形,得OF=AE=4cm,由垂径定理得:DF=3,根据勾股定理求半径OD的长.
解答 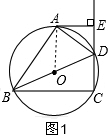 (1)证明:连结OA,
(1)证明:连结OA,
∵OA=OD,
∴∠ODA=∠OAD,
∵DA平分∠BDE,
∴∠ODA=∠EDA,
∴∠OAD=∠EDA,
∴EC∥OA,
∵AE⊥CD,
∴OA⊥AE,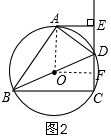
∵点A在⊙O上,
∴AE是⊙O的切线;
(2)过点O作OF⊥CD,垂足为点F,
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形,
∴OF=AE=4cm,
又∵OF⊥CD,
∴DF=$\frac{1}{2}$CD=3cm,
在Rt△ODF中,OD=$\sqrt{O{F^2}+D{F^2}}$=5cm,
即⊙O的半径为5cm.
点评 本题考查了切线的判定和性质,在判定一条直线为圆的切线时,分两种情况判定:①当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径即可,②当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,此题属于第二种情况:连接OA,是半径,证明垂直即可.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
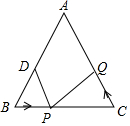 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为3或2时,能够在某一时刻使△BPD与△CQP全等.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为3或2时,能够在某一时刻使△BPD与△CQP全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
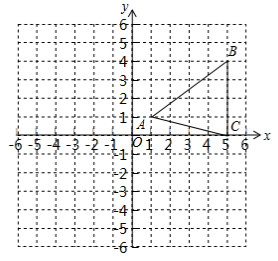 如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).
如图,在平面直角坐标系中,△ABC的顶点为A(1,1),B(5,4),C(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com