
分析 ①根据方法①,先转化为同指数幂相乘,然后逆运用积的乘方的性质进行计算即可得解;
②根据方法②,逆运用乘法分配律进行计算即可得解;
③根据方法③,先将除法转化为乘法,然后利用乘法分配律进行计算即可得解;
④根据方法④,先裂项,然后进行计算即可得解.
解答 解:①(-0.125)2016×(-8)2017,
=(-0.125)2016×(-8)2016×(-8),
=[(-0.125)×(-8)]2016×(-8),
=-8;
②$\frac{4}{7}$×(-$\frac{5}{23}$)-(-$\frac{3}{7}$)×(-$\frac{5}{23}$)-$\frac{5}{23}$×2$\frac{2}{7}$,
=$\frac{4}{7}$×(-$\frac{5}{23}$)+$\frac{3}{7}$×(-$\frac{5}{23}$)+(-$\frac{3}{25}$)×2$\frac{2}{7}$,
=(-$\frac{5}{23}$)×($\frac{4}{7}$+$\frac{3}{7}$+$\frac{16}{7}$),
=(-$\frac{5}{23}$)×$\frac{23}{7}$,
=-$\frac{5}{7}$;
③(-2015$\frac{5}{8}$)÷(-5),
=2015$\frac{5}{8}$×$\frac{1}{5}$,
=(2015+$\frac{5}{8}$)×$\frac{1}{5}$,
=2015×$\frac{1}{5}$+$\frac{5}{8}$×$\frac{1}{5}$,
=403+$\frac{1}{8}$,
=403$\frac{1}{8}$;
④$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$,
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$,
=1-$\frac{1}{2017}$,
=$\frac{2016}{2017}$.
点评 本题是对数字变化规律的考查,读懂题目信息,理解各种简便运算方法的操作是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-4)2>(-3)2 | B. | |-4|>|-3| | C. | -4>-3 | D. | $-\frac{1}{4}$>$-\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:在数学课上,老师请同学思考如下问题:
阅读下面材料:在数学课上,老师请同学思考如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,同一时刻在阳光照射下,树AB的影子BC=3m,小明的影子B'C'=1.5m,已知小明的身高A'B'=1.7m,则树高 AB=3.4m.
如图,同一时刻在阳光照射下,树AB的影子BC=3m,小明的影子B'C'=1.5m,已知小明的身高A'B'=1.7m,则树高 AB=3.4m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
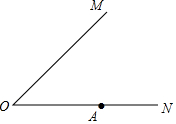 已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).
已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P 到∠MON两边的距离相等.(请用尺规作图,保留作图痕迹,不要求写出作法,不必证明).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com