
分析 (1)直接利用完全平方公式分解因式得出答案;
(2)将前两项和后两项分组提取公因式得出答案.
解答 解:(1)x2-y2-x+3y-2
=(x2-x+$\frac{1}{4}$)-(y2-3y+$\frac{9}{4}$)
=(x-$\frac{1}{2}$)2-(y-$\frac{3}{2}$)2
=(x-$\frac{1}{2}$-y+$\frac{3}{2}$)(x-$\frac{1}{2}$+y-$\frac{3}{2}$)
=(x-y+1)(x+y-2);
(2)6xy+4x+3y+2
=2x(3y+2)+(3y+2)
=(3y+2)(2x+1).
点评 此题主要考查了分组分解法分解因式,正确分组是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
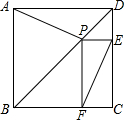 如图,P是正方形ABCD对角线BD上的一动点(不与B、D重合),PE⊥DC,PF⊥BC,E、F分别为垂足.
如图,P是正方形ABCD对角线BD上的一动点(不与B、D重合),PE⊥DC,PF⊥BC,E、F分别为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
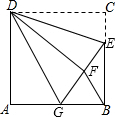 如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号)
如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com